Bert hamminga DME applied to Supply and Demand   000213  Supply and Demand       

Statics: The Definition Of Equilibrium.                    Comparative Statics           Dynamics

 The central static IT in supply and demand theory is (suffix "s1" stands for statics 1):

IT_s1: there is one and only one equilibrium point ("existence and uniqueness").

The basic conditions C_i  in the PET1:

PET_s1: {C₁,C₂,...,C_k} � IT_s1

are:
HC₁: q = S (p)
HC₂: q = D (p)

These are HC conditions. They are conditions on (p,q)'s. Some (p,q)'s satisfy the condition  q=S(p), like (p,q)_s1 and (p,q)_s3, others do not, like (p,q)_s2.
C₁ and C₂ reflect the economist's basic idea that under "perfect" conditions (perfect information, a single homogenous good with no substitutes of complementary goods etc. etc.), the equilibrium  is a value of (p,q) satisfying C₁ and C₂.
These HC conditions are insufficient to proove IT. There are many exceptions.You need special conditions to exclude the exceptions. (This example is pure Hard Core analysis: it has no application conditions as usually found in DME). These are examples of S-D pairs that we do not want (Philosopher of Science Imre Lakatos calls such undesired counterexamples monsters):

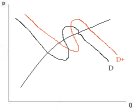M Monster 1 (left): If the supply curve, like the black D or the red D+ is wave-shaped like in the picture right, you can have up to three equilibrium points. A rough measure to exclude such problems is to linearize like in special condition SC1:

SC_s1:     q= S(p) = ap+b, q= D(p) = cp+d

When a problem is too complex, linearization is often the first step in deductive model exploration. In later stages, one tries to drop this strong condition.

M Monster 2 (right): If S=D, there are infinitely many equilibrium points.
If S and D' are parallel lines, you have no equilibrium point. Under linearity, monster 1 can be excluded by the special condition SC2 ("<>" means unequal):

SC_s2: a<>c

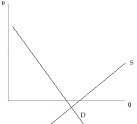.M Monster 3 (right):  You do not want an equilibrium at a negative price. Under the linear equations introduced to bar monster 1, S=D iff ap+b=cp+d. So the special condition SC3 we need to introduce is:

SC_s3: p = (d-b) / (a-c) > 0

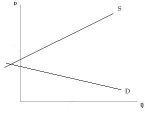M Monster 4 (left): You do not want an equilibrium at a negative quantity. Under the linear equations introduced to bar monster 1

SC_s4: q = (ad-cb) / (a-c) > 0

Summarizing: we may at first have thought that existence and uniqueness of equilibrium on a single homogenous market with no substitutes, nor complementary goods under perfect information etc. etc. was pretty obvious. We ended up with linearizing, a very strong special condition SC1, and special conditions SC2, SC3 and SC4 on the values for the parameters a,b,c and d in order to bar monsters 2, 3 and 4.  This is sufficient for existence and uniqueness. The PET runs like this:

PET_s1:  {HC₁,HC₂,SC_s1,SC_s2,SC_s3,SC_s4}� IT_s1

After establishing a first version of such a PET as just explained, DME

• trying to derive IT after dropping SC_s1 (linearity) and thus proving existence and uniqueness for the widest possible class of S and D functions (weakening of conditions and alternative conditions).
• trying to derive IT by introducing a second commodity, the price of which influences the market of the first commodity (substitutability and complementarity). This is field extension.
• finding the conditions "behind" the demand and supply curves (deriving D and S from utility maximation, profit maximation, budget constraints). In the explanation of DME we have called results in this direction: conditions for conditions results.

Comparative statics            Statics    Dynamics

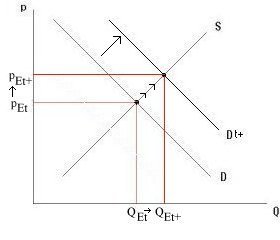Comparative static analysis of changes: IT concern whether new equilibrium values (p,q) will be higher or lower if some exogenous variable t gets higher or lower. So, IT state that

Dp /  Dt

is positive (or negative), and the possibly the same  with  Dq /  Dt.

Those are classical examples of a comparative static theorems:
IT_cs1: Dp /  Dt > 0
IT_cs2: Dq /  Dt > 0
If in the neighbourhood where (p,q) is going to move as a result of the t-shock the following special conditions hold (for the explanation click here):

SC_cs1: dS / dp > 0 (S is upward sloping to the right)

SC_cs2: � D / � t > 0 (Demand rises if, ceteris paribus, t rises)

SC_cs3: Equilibrium exists and is unique (our statical IT from the previous paragraph!)

That means p_E and Q_E move in the same direction as t, on warmer days, more ice is sold more expensively. So we have two PET's:

PET_cs1:  {HC₁,HC₂,SC_cs1,SC_cs2,SC_cs3,}� IT_cs1
PET_cs2:  {HC₁,HC₂,SC_cs1,SC_cs2,SC_cs3}� IT_cs2

Those are classical examples of a comparative static theorems.
In statics we prefer equilibrium to exist and to be unique because that is a very useful condition to use in comparative statics. Multiple (not unique) equilibria like in Monster 1 cause serious problems: If before the t-shock the (p,q) equilibria are possible, and after the t-shock again three, from where to where would the equilibrium-(p,q) go? There are 9 possibilities, not likely al to  yoield the same sign for Dp /  Dt   or Dq /  Dt. You're not likely to deduce any interesting theorem. But linearization, as we did here, is an unneceesarily heavy poison for the monster. Weaker conditions will do. We shall not go into the details. These examples serve the purpose to make clear to you how DME goes about in general.

Dynamics: the Path to Equilibrium:              Statics         Comparative Statics

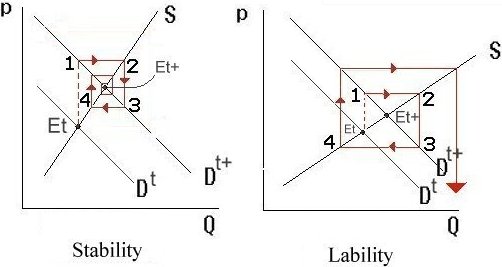
In initial situation 1, suppliers face a demand at which they had wished to supply a quantity according to point 2. They go home dissatisfied and make new plans for the next day. The second day, they supply a quantity according to 2, but discover that, at that quantity, they can only clear their market if they sell sell at a price according to 3. The third day, they sell a quantity belonging to their supply curve at the price of 3, that is, according to 4. Whether or not supplier's decisions will thus approach market equilibrium, depends on the slope of S relative to D. In the right hand side graph, these slopes are such that the market gets out of hand ("explodes").

The aims of dynamics are to find out

• whether or not equilibrium will settle (whether or not the system is stable)
• what determines the speed by which the new equilibrium will be attained.

If stability is an IT (called IT_d1), what would be the special conditions for stability in this case? Under what general conditions do we get result like the left had side graph, under what conditions do we get results like the right hand side graph? In the case of linear S and D, the special condition SC_d1 on the linear functions S and D is:

SC_d1: dS/dp <  - �D/�p

As a memory aid remember: to avoid an explosion, suppliers S should not overreact on demanders D. Summarized in the metalanguage of DME:

PET_d1:  {HC₁,HC₂,SC_d1}� IT_d1

Dynamics needs comparative statics, comparative statics needs statics

Finally: you have now seen that for comparative statics you need the basic statical results of existence and uniqueness. For dynamics: to follow the time paths towards the new equilibrium comparative statics should first tell you to what final destination the time path is leading.