Contents: Introduction Structure and development of the theory of consumer behaviour Plausibility The relevance of econometric tests Concluding remarks Figure 1 Conceptual worlds Figure 2 Weakening of conditions Figure 3 Lancaster's theory development

1. Introduction

It has by now become widely recognized that economists show ambivalent behaviour. The relation between what they say to do and what they really do in their daily professional life is, to say the least, ambiguous. This ambivalence has been noted by several authors, for example Blaug (1980), Klamer and McCloskey (1988) and hamminga (1983). In the instrumentalistic/falsificationistic spirit of Friedman and Machlup, who succeeded in convincing their colleagues of their methodological canons, economists stress the importance of submitting theories to empirical tests. This explicit methodological belief however, stands in sharp contrast with the way economists actually behave in daily practice (their implicit methodology): empirical tests appear to have no influence on the development of economic theories at all.

In this paper the implicit methodology of economists will be unveiled by giving an account of the developments that have taken place in the neo-classical micro-economic theory of consumer behaviour. It will be shown that, as one might expect, the developments in this theory are not guided by the results of empirical tests. Far less obvious, however, is the proposition that theoretical research is guided in a quite specific way by plausibility-driven development strategies, that is, strategies based on plausibility convictions which consist of introspective evidence and common sense knowledge. In this respect it can be concluded that economists nowadays use the method of the apriorists which found its last defender in Lionel Robbins (1934). Later methodological discussions did not alter this adherence to apriorism and led primarily to muddling the relation between explicit methodological canons and the implicitly day to day methodology. It is maybe for this reason that methodological discussions have sometimes looked so unfruitful in the eyes of practising economists.

Therefore in this paper a meta-theory of economic theory structure and development will be laid out which describes the implicit methodology of economists. It will explain its inner logic and give reasons for its use instead of the use of some explicit methodology which is supposed to be based on empirical testing. It explains why theoretical economists are in a way `forced' to adopt this methodology. The meta-theory will be illustrated by examples taken from the developments in the theory of consumer behaviour. Much of this meta-theory was already put forward by hamminga (1983) in his study of the developments in the Heckscher-Ohlin research programme on international trade. The ideas stated here can be seen as a further elaboration of and improvement upon his meta-theory by applying it to the theory of consumer behaviour. It is hoped that herewith a contribution is made towards a methodological discussion which is valuable in itself but could, more importantly, also be relevant again for practising economists.

In the following section the meta-theory concerning the structure and development of economic theory will be presented. It will be shown that this meta-theory describes the developments in the theory of consumer behaviour adequately and reveals their logical structure clearly.

Next, in section three, a plausibility hypothesis is ventured as an answer to the question why the theoretical developments took place the way described in the previous section. This hypothesis states that economists try to raise the plausibility of their theories as much as possible by proving old theorems for an increased number of possible worlds, or by introducing new plausible theorems. It is shown that the ways in which the theory is developed (the strategies used by economists) are indeed plausibility heightening. Typically the implicit method thus described enables theorists to agree about theoretical progression without considering econometric and other empirical evidence. This is even the case when they differ in opinion about which propositions should be called plausible, and which should not. Therefore this method can be called `empirically immune', in full contrast to the professed methodological canons which are explicitly empirically based.

In section four the problematic nature of econometric tests of economic theories is treated and illustrated by examples of performed tests of the theory of consumer behaviour. The main problem is that econometricians are forced to make all kinds of, only vaguely known, auxiliary hypotheses in order to perform a test, thereby drastically limiting its relevance for theoretical research. Once this is established the conclusion follows naturally that theoretical economists are `forced' to adopt a method which is not empirically based, but has its own inner logic, independent of empirical results. As will be shown the plausibility-driven development strategies used by theorists possess this inner logic, geared at some kind of search for the `truth'.

With the introduction and application of the (marginal) utility-concept in economic theorizing around 1871, Walras, Jevons and Menger started off a new research programme concerning consumer behaviour. Their main goal was somehow to give a foundation for the well known and much used law of demand, stating that demand curves do not slope upward. This analysis became known as the traditional theory of consumer behaviour: assuming utility maximizing behaviour and given an additive utility function, prices and income, they proved theorems such as the first law of Gossen (the equimarginal principle) and the law of demand. Hicks and Allen (1934) were the first to improve on these ideas. Dissatisfied with the implied measurement of the cardinal additive utility-function they introduced the more general so called ordinal, generalized utility-function, deducing the Slutsky-equation wherein the price-effect on a quantity demanded was divided into a substitution-effect and an income-effect. The sign and magnitude of the income-effect was uncertain and therefore the price-effect also. But they did prove restrictions on the substitution-effect: the substitution matrix, consisting of partial derivatives of the demand of goods with respect to their prices, was proved to be a symmetric and negative semi-definite matrix. From this result they derived, with an additional condition concerning the sign of the income-effect (the condition of the good being `non-inferior'), the law of demand.

Samuelson (1938a, 1938b, 1948, 1950), defending his views in terms of the methodology of operationalism at that time, tried to prove the results of Hicks and Allen from observable statements only. He took market behaviour as a starting point and introduced the weak axiom of revealed preference. He succeeded in proving the symmetry and negative semi-definiteness of the substitution-matrix, but only in the case of two goods. His work is finished off by Houthakker (1950) who, by using his strong axiom of revealed preference, managed to prove the Hicks and Allen results for an arbitrary number of goods. From that time on the axiomatization of the theory of consumer behaviour using the set-theoretical approach began, the first contribution made by Debreu (1959) soon followed by others (for example Uzawa (1960) and authors in Chipman and all (1971)). Another direction was taken by Lancaster (1966) who introduced his theory of characteristics with which he was able to prove theorems in addition to the results of Hicks and Allen.

These developments in the theory of consumer behaviour can be described in terms of a meta-theory which was originally developed by hamminga (1983). The basic idea of this meta-theory is that economic theory is centred around deductive proofs of so called Interesting Theorems (IT). Interesting theorems are theorems with a clear economic meaning, preferably statements with policy-implications (containing for instance macro-economic advice for the government or strategies for optimal firm-behaviour), or which are congruent with established opinions held by economists in the field (for example a negatively inclined demand curve for a good). Deductive proofs consist of a set of conditions (also called hypotheses or assumptions) from which a conclusion is deductively derived, that is, given the conditions to be true, it follows necessarily that the conclusion (the theorem) is also true. Therefore the structure of these proofs can be represented as follows

(1) V (C₁,......,C_k => IT)

This is called a proposition of economic theory (PET). It should be read as follows: the set of conditions C₁,..,C_k is sufficient to prove an interesting theorem IT in a field V. The field specifies the kind of entities the theorem deals with and their numbers (e.g. two goods, three consumers, one firm, two countries etc.). Theory-development takes place by altering the conditions of the PET, but still proving the same IT, thereby raising its plausibility, or leading to the introduction of a new IT.

An example of an IT that is proven in the traditional analysis of consumer behaviour is the first law of Gossen (also known as the equimarginal principle, stating that the ratios of the marginal utilities (MU_i) of goods and their prices (p_i) are the same for all goods: MU_i/p_i = b for all i, with b some constant). Walras, Menger and Jevons succeeded in proving this interesting theorem for a certain set of conditions by means of deductive reasoning.

The set of conditions C₁,..,C_k under which a theorem is proved can be divided in three sub-classes: conditions resulting from the use of a certain foundation of economic analysis (abbreviated by FEA), resulting from the use of a certain explanatory ideal (EI) and Technical Conditions (TC). (The terms will be explained below.) These classes are denoted in a PET by FEA_1-i, EI_1-j and TC_1-k (with i,j and k counting respectively the number of FEA-, EI- and Technical conditions). These classes are distinguished because each class of conditions plays a different role in theory development, and originates from different sources, thereby differing in its importance in the eyes of economists.

1. FEA-conditions. These are conditions resulting from the use of a certain foundation of economic analysis (FEA). One can differentiate between a classical Ricardian FEA (based on the concepts of labour value), and a neo-classical FEA which is based on maximizing behaviour of economic agents. The neo-classical FEA in this case reads as: the consumer buys his utility maximizing bundle of goods. This condition is denoted by FEA₁. A FEA constitutes the basic starting point of analysis in a research programme and can be seen as an empirical analogon to a Lakatosian `hard core', in the sense that it is not assailable and that it is fundamental for a research programme. Changing the FEA will start off a new research programme. For instance the switch from classical to neo-classical analysis started off new research programmes in almost all domains under economic study.

2. EI-conditions. These are conditions resulting from the use of a certain explanatory ideal (EI) within a research programme. While the FEA constitutes the starting point of analysis, the EI gives the direction in which an explanation for economic behaviour is sought. Just as the introduction of a new FEA starts off a new research programme, the introduction of a new EI results in a new theory within the same research programme. A theory can be seen as a set of PET's containing the same EI-conditions and I will use the term theory in this sense throughout the rest of the paper. In the research programme concerning consumer behaviour, economists speak of the traditional utility theory, the Hicks and Allen theory and the theory of revealed preference, each theory having its own explanatory ideal, and therefore its own specific EI-conditions.

In traditional utility theory the EI is to explain the behaviour of the consumer given his preferences and his income. Making this ideal operational, four conditions were made:

EI₁: given a cardinal additive utility function (u),

EI₂: given a completely spent income,

EI₃: given prices of goods, and

EI₄: given the possibility for the consumer to buy all bundles of goods as long as his income is sufficient.

3. Technical conditions. These are the other conditions besides the FEA- and EI-conditions which are necessary to derive the theorem. They are of a technical nature (therefore called Technical Conditions) and economists are not particularly attached to these conditions. They are unimportant, and changing them would not cause much disturbance, unlike changes in the EI, let alone in the FEA. In the traditional utility theory the technical conditions are restrictions on the utility-function u:

TC₁: u > 0 (each good is valued positively),

TC₂: u' > 0 (the consumer is non-satiable),

TC₃: u'' < 0 (the so called `law' of diminishing marginal utility), and

TC₄: continuity of u, u' and u''.

The sets of FEA-, EI- and Technical conditions taken together are sufficient to prove the equimarginal principle (denoted by IT₁) in the case of an arbitrary number of goods (n) indicated by V_n. V_n stands for field, the index counting the number of the entity about which the theorem is to say something, in this case goods. V can be called one-dimensional in this case but it could in principle also have more dimensions. This would be indicated by more indices, counting for instance the number of firms, countries, production factors etc. which the theorem deals with. However, these dimensions are irrelevant in the traditional theory of consumer behaviour and therefore not indicated. The PET which is proved can be represented by

(2) V_n (FEA₁, EI_1-4, TC_1-4 => IT₁)

The equimarginal principle (IT₁) determines the utility maximizing bundle of a consumer. It is purely static and tells nothing about the change in consumer behaviour as a result of a change in prices or in income of the consumer. By comparing the static solution before a change in prices or income with the static solution which occurs after a change has taken place, `dynamic' theorems can be proven (comparative statics). One of these `dynamic' theorems is the famous law of demand, which is also an important theorem in the traditional utility theory, besides the equimarginal principle. Marshall proved this law, that is, he proved the demand curve for a good to be negatively inclined, under the conditions mentioned above combined with two extra conditions, an EI-condition (because it originates from the use of the EI):

EI₅: income and prices of all other goods are constant,

and a technical condition:

TC₅: the marginal utility of money is constant.

If the law of demand is called IT₂, Marshall's result can be represented by

(3) V_n (FEA₁ , EI_1-5 , TC_1-5 => IT₂)

Having analyzed the structure of the propositions of the traditional analysis it is now possible to describe in the same terms the developments which have taken place in the research programme concerning consumer behaviour, after the introduction of the traditional utility theory. These developments can be categorized in three classes. Each class will be illustrated by some brief examples from this research programme. For a more extended treatment see Timmer (1995).

Three forms of theory-development can be discerned in this research programme. They are called development strategies, because these forms are deliberately used by economists to develop some theory. The strategies are:

1. finding a new set of conditions,

2. field extension, and

3. introduction of a new theorem.

The first two strategies concern the proving of an old IT under a new set of conditions or for a new, extended, field, whereas the last strategy concerns the proof of some new theorem, arising from changes made in the old set of conditions. The last development strategy was not found by hamminga in his study of the theory of international trade. In this research programme all attention was directed to proofs of the same basic theorems, see hamminga (1983).

ad 1. This strategy starts from some already proven PET in which a certain IT was proven under certain conditions. It aims at proving the same IT under a new set of conditions by replacing some of the old conditions. This new set can be arrived at in three ways (as described in hamminga (1983, pp. 66-69)): 1a. by weakening of conditions, 1b. by giving alternative conditions and 1c. by giving conditions for conditions. Weakening of conditions means proving a theorem under weaker conditions, that is, extending the domain of the theorem by proving it for a new set of conditions which can be deduced from the old set, but not the other way around. Mostly this kind of development is directed to one condition which is weakened. An other form of domain extension is reached by giving alternative conditions. This means proving the theorem for completely new situations whereby (in contrast with weakening of conditions) the old situations are not included. Conditions for conditions do not extend the domain of a theorem, but are often given to clarify the economic meaning of some conditions by giving new, economically meaningful conditions which are sufficient for some unclear condition, and thereby replace it.

The replacing of conditions takes place on three levels, according to the three classes of conditions mentioned above. The highest level is the level of the Foundation of Economic Analysis (FEA). Replacement of a FEA starts off a new research programme as was the case with the introduction of the utility-maximizing postulate in the study of consumer behaviour, which led to a new, neo-classical research programme in contrast with the classical analysis. This kind of theory-development is of course very rare. FEA-conditions are never weakened or partially altered in an other way (by giving alternative or conditions for conditions), they form the `hard core' to which `all or nothing' applies by definition.

The second level at which condition replacing takes place is the level of the Explanatory Ideal (EI). An example of the weakening of a set of EI-conditions is the work of Hicks and Allen (1934). They objected to the use of a cardinal utility function (as was done in the traditional analysis) which implies measurement of utility and took unmeasurable generalized utility functions as a starting point: preference orderings, represented by a set of indifference curves. With this they were able to proof the old IT's of the traditional theory like the equimarginal principle and the law of demand. Because every cardinal additive function is also an ordinal generalized one, but not the other way around, Hicks and Allen can be said to have weakened the set of EI-conditions of the traditional analysis.

An example of the attempt to give alternative EI-conditions is the result of Houthakker (1950). Samuelson (1938a,b) objected to the use of unobservable entities and introduced a new explanatory ideal were not the unobservable preference ordering of Hicks and Allen, but observable market behaviour functions as a starting point for explaining consumer behaviour (the method of revealed preference). After his preliminary work Houthakker comes up with a new central EI-condition in this kind of analysis: the strong axiom of revealed preference. With this axiom Houthakker proves the main results of Hicks and Allen, i.e. the symmetry and negative semi-definiteness of the substitution matrix. However, it was shown afterwards that Houthakker's conditions could be proved from those of Hicks and Allen, and vice versa. They appeared to be equivalent and therefore this result cannot be called alternative but should be considered as a complete conditions for conditions result. It was recognized that Houthakker's set of conditions was more comprehensible, having a clearer economic meaning than the set of Hicks and Allen.

The lowest level of replacement of conditions is the level of technical conditions. This low-level theory development took for instance place in the period of the axiomatization of the Hicks and Allen theory in terms of preference relations. An example of a technical condition weakening is the result of Hurwicz and Uzawa (1971) who claim to prove a symmetric, negative semi-definite substitution matrix without the inversion condition which Samuelson needed, or the result of Hurwicz (1971) who weakens the differentiability conditions which Hicks and Allen needed to prove their theorems. A conditions for condition result was arrived at by for example Sonnenschein (1971) who replaces the transitivity condition in the proof of the Hicks and Allen results by some technical assumptions about the convexity and semi-continuity of the preference relation.

Typically changes in the set of conditions at a certain level lead often to changes at other levels. There is a certain hierarchy: the changing of conditions at the highest FEA-level also brings about changes at the lower EI- and TC-level. And a change at the EI-level brings about changes in the set of Technical Conditions: they have to be adapted to serve the new explanatory ideal. One could speak of a domino-effect. A good example of this effect is the weakening of the traditional EI carried out by Hicks and Allen. They weakened the EI-condition of an additive utility function by replacing it with a generalized one. But in order to still prove the law of demand, they were forced to introduce a new technical condition alongside the old ones, namely the condition of a non-inferior good. In some special cases, inferior goods could lead to rising demand curves. Therefore the law of demand does not unconditionally hold when these goods are not excluded (see Hicks (1939), p.28).

ad 2. An other theory development strategy is field extension. Field extension means the extension of the field in which a certain theorem can be proved. This extension can take place in two ways: by raising the number of entities of a certain kind, or by extending the number of kinds of entities (dimensions of the field). An example of the first kind of field extension is the theory development from Samuelson (1938a,b) to Houthakker (1950). It was shown that Samuelson's weak axiom of revealed preference was sufficient for proving the Hicks and Allen results but only in the case of two goods. Houthakker extended the field by introducing his Strong Axiom instead of Samuelson's Weak one, and proved the symmetric and negative semi-definiteness of the Slutsky-matrix for an arbitrary number (n) of goods. An extension of the dimensions of a field took place for instance with the introduction of Lancaster's theory of characteristics (Lancaster (1966)). Besides the number of goods, the number of characteristics became important in his theory (denoted by an extra index, say m: V_nm). An other example is the introduction of time in intertemporal consumer analysis. In this analysis the number of periods constitutes a new dimension, besides the number of goods.

Field extension always brings about changes in the set of conditions because the conditions have to serve for a greater domain. In the first case Samuelson's weak axiom was replaced by Houthakker's strong one. And Lancaster needed new conditions concerning the characteristics he introduced.

ad 3. The above mentioned theory development strategies were directed towards proving the same theorems under a new set of conditions or for an extended field. However, it can also be the case that the changing of conditions results in the proof of new interesting theorems. This is clearly the case from the transition of the traditional theory to the Hicks and Allen theory. After the introduction of the generalized utility function it became meaningful to speak of cross-elasticities of demand (which were always zero in the traditional analysis because of the additive utility function). Hicks and Allen proved the symmetry and negative semi-definiteness of the substitution matrix, results which were not arrived at in the traditional analysis but became extremely important afterwards. Another example is Lancaster's theory of characteristics: besides the Hicks and Allen results he proves new theorems like the displacement of a good from the market by the introduction of a new good.

By now, I have laid out a meta-theory which describes adequately the structure and development in the theoretical research programme concerning consumer behaviour. This meta-theory is valuable in itself but gives only a description. What we would like to have is also some kind of explanation. In the following section an attempt will be made to give this explanation of the way economic theory develops in terms of plausibility.

3. Plausibility

The central and most interesting question remains to be answered. Why do economists behave in the way described above, that is, why do they follow the three forms of development strategies? What is the goal they are aiming at by proving theorems under new sets of conditions, for extended fields or by introducing new theorems? What is their driving force? First of all it should be noted that results of empirical tests do not influence the way the theory of consumer behaviour is developed. Nowhere in the writings of the participants in this research programme can any reference be found to empirical tests. In no case is a new proposition of economic theory proven by a author because some conditions of an old PET or a proven theorem were in some way found to be falsified in empirical tests. No matter what Friedman, Machlup or other post-Robbins methodologists might have said, economic theory development is neither led by the testing of its theorems nor of its assumptions. But what is the driving force if it is not empirically testing?

hamminga (1983, p.71) ventured his plausibility-hypothesis: `economists try to raise the plausibility of emerged interesting theorems as high as possible.' This hypothesis will be used here as a starting point but has to be extended later on to fit the developments in the theory of consumer behaviour. Plausibility is a concept often used in economic literature but rarely defined. It is used here in the sense of `congruence with common sense knowledge and introspective evidence', called plausibility convictions. These plausibility convictions have several characteristics. First of all they are directed to statements: one has a common sense conviction about the plausibility of a certain statement like: a consumer is insatiable or the demand for a good is negatively related to its price. Further they are not static: plausibility convictions change over time. Thirdly, plausibility convictions are often connected with other plausibility convictions.

In this paper it is claimed that developments in economic research programmes are directed by these convictions. Take for instance Hicks and Allen (1934). They introduced a generalized utility function not because of some falsification of the traditional results or assumptions, but because a generalized function is mathematically more general and because it was congruent with introspection: the utility of a commodity cannot be considered to be independent of the quantity of other commodities consumed (e.g. bread and butter). And for example Houthakker did not improve upon Samuelson by proving the Hicks and Allen results for n goods instead of for 2 because tests `falsified' Samuelson's theory, but because common sense suggests that in the real world there are more than two goods. In the same way Lancaster formulated his theory of characteristics not because of the fact that after empirical investigation substitution matrices turned out to be not symmetric at all, but because he thought the Hicks and Allen theory had nothing to say about quite common real life happenings, like the change in consumer behaviour after the introduction of a new good. And also because of the introspective fact that a consumer does not appreciate the good per se but that it is the characteristics of a good from which his utility is derived.

An illustration of the non-static character of plausibility convictions is provided by the `disappearance' of the law of demand. The main task the three founders of neo-classical consumer theory set themselves, was to give an `explanation' of the law of demand, which they all regarded as highly plausible. Hicks and Allen also took great pains to be able to prove this law, making an extra condition of non-inferior goods. However, with the arrival of Samuelson in the field, the law of demand lost its plausibility. Samuelson explicitly stated that he was not at all interested in its `explanation'. Attention was shifted away to other theorems like the symmetry of the Slutsky-matrix. Somehow the law of demand `lost' its plausibility in this period.

Another characteristic of plausibility convictions is their network character. Convictions are connected with each other, that is connected with convictions derived from other (well-supported) theories (see also Nooteboom (1986)). So plausibility judgments do not have to be directly based on common sense grounds, but they can also be grounded in the plausibility of (parts of) other theories. A good example of this is the plausibility of the new economics of the family which derives its plausibility by making use of the Hicks and Allen framework of analysis. These plausibility connections are not only confined within a scientific domain, but also cross the borders between the different sciences. Physics has always been an ideal for economists, and e.g. Mirowski (1989) claimed that the traditional utility theory owns its plausibility mainly from the fact that it is created in analogy to nineteenth century physics: a theory of forces which was (in that time) very successful in the eyes of physicists nd (thereby) economists. An other good example is the use of Darwin's evolutionary theory in the emerging field of the socalled evolutionary economics.

Now we have seen just what plausibility convictions look like, it is possible to assess the role they play in theory development, taking the plausibility hypothesis of hamminga, as a starting point. This hypothesis states that `economists try to raise the plausibility of emerged interesting theorems as high as possible.' Plausibility convictions express the beliefs of economists about economic phenomena in the world. `Raising the plausibility of a theorem' means then making a theorem more `realistic' in their eyes. More plausible means: a greater chance to be true in the real world, where real world means just one of the worlds that can be described in the economists' language. The Venn-diagram in Figure 1 will clarify this.

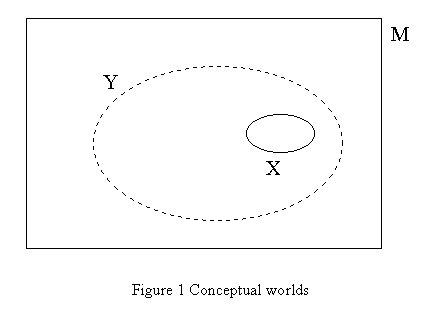
Let M be the set of all conceptually possible worlds for a theory, that is all the worlds that can be described in terms of the language of economists. An example of M is the set of worlds determined by all possible combinations of incomes, prices and preference orderings of a consumer. A statement like `all preference orderings are additive' determines a subset in M which excludes all worlds in which preference orderings are not additive.

Given some interesting theorem (IT) we can say that for some worlds in the set M this theorem is true, but we do not know for which worlds. This subset of M, called Y, is unknown to us, therefore it is represented in the diagram by a broken line. We would like to know the set of worlds in which the theorem holds true. This set of worlds can be called the target-set. Knowing all worlds in this target-set is the ultimate goal of theorizing. By proving the theorem for a set of conditions as described in a PET some worlds where IT is true become known to us: these worlds are indicated by subset X. X is the set of all worlds which satisfy the conditions under which the interesting theorem has been proven, it is the result-set. Because in all worlds of X the theorem is proved to be true (by deductive reasoning), X is a subset of Y: all elements of X are necessarily elements of Y but there may be worlds, yet unknown, in which the theorem holds true also, so not all elements of Y are necessarily elements of X. Assuming that economists take their theorizing seriously, we may conjecture that one of the conceptually possible worlds in M, say w_a, is the nearest theoretical description of the real, `actual' world. This world however is not known. All that economists have are their convictions about the plausibility of certain worlds, which can be seen in the light of the above discussion as convictions about the plausibility of a certain statement being true in the real world. Therefore plausibility convictions can be formalized as a probability function which I call PL, the plausibility function. Let A and B be subsets of the set of all conceptually possible worlds M then the function PL should fulfil the following conditions

PL(A) gives the plausibility of set A: the chance that the `actual' world is an element of A. It can now be easily seen (because of condition (iii)) that enlargement of the set X (in Figure 1) means heightening its plausibility: the chance that w_a is an element of X is raised. By enlarging set X under which a theorem can be proved, the set of worlds in which the theorem is known to hold is also enlarged, consequently the plausibility of the theorem is heightened. This is exactly what hamminga, according to his plausibility hypothesis, believes to be the objective of economists.

With this formalization of the plausibility concept two interpretations of the plausibility concept can be distinguished which I will denote by objective plausibility and subjective plausibility. Objective plausibility means that each world w of M is considered to be equally plausible, that is, the chance the actual world w_a being the same as w is equal for all w. Let the number of possible worlds in M be N, and in A N(A), then the plausibility function defined in (1) can be described further as

(2)

 In this case the plausibility of a hypothesis depends only on the number of possible worlds which fulfil the hypothesis. In contrast with objective plausibility, subjective plausibility means that not each world is considered to be even plausible, but that a difference in plausibility valuations of possible worlds exists: some worlds are considered to be more plausible than others.

The last case is probably a more adequate description of what is in the mind of economists. But the remarkable thing about this way of thinking is that for economists to come to an agreement about considering a new theory to be more plausible than an old one, discussions about plausibility convictions are completely superfluous when the new theory is developed according to one of the strategies mentioned in section two. No matter what plausibility function an economist holds (be it the objective or some subjective one): when a new theory is developed by giving weaker conditions, alternative conditions, conditions for conditions or field extension, the new theory is more plausible. This will be shown in the following.

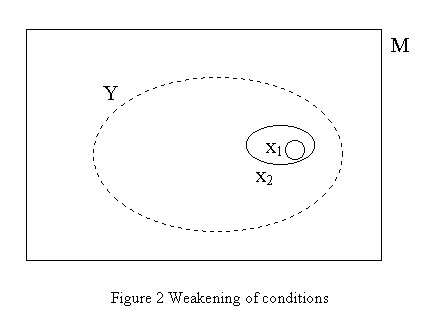
It can be seen easily that weakening the conditions under which a theorem can be proven to be true is equal to enlarging the set of theoretical possible worlds X for which the theorem has been proven to be true. Weakening a set means including more worlds, see Figure 2 in which the set X₁ is weakened to X₂. Therefore the plausibility of X₂ is at least as large as the plausibility of X₁ (because of 1(iii)), no matter the exact shape of function PL. It should be noted that this kind of theory development is just the opposite of what according to Popper constitutes sound scientific progress because by the weakening of conditions it becomes less easy to falsify the theory, it leads to a decrease in empirical content, where Popper argues in favour of an increase.

In the same way field extension by raising the number of a certain kind of entity (goods, consumers, firms, etc.) leads to more plausibility, because it enlarges X analogously to the weakening of conditions. Plausibility evaluations in the case of an increase in the number of field dimensions are more complicated and will be treated below when the theory development of Lancaster is described.

The proof of a theorem under alternative conditions can also be seen to raise plausibility: by proving the theorem for some new worlds not included in the old X, the number of worlds in which the theorem is known to hold true is raised, and thereby its plausibility.

The giving of conditions for conditions can be said to raise the plausibility in some other way. Judgments of plausibility apply to statements but before reasonable judgment is possible the statement should be economically meaningful. Suppose economists do not have a clear intuition about the plausibility of (a set of) conditions. When this (set of) conditions can be replaced by an other set which does have clear economic meaning one can speak in a way of an increase of plausibility. So, although Houthakker's conditions ultimately are the same as those of Hicks and Allen, his conditions, which are stated in terms of observable market behaviour, have a clearer economic meaning than the Hicks and Allen conditions which contain an unobservable utility function.

The above treated kinds of theory development are directed to the proof of the same theorem under a new set of conditions. For explaining the third kind of theory development strategies, the introduction and the proof of a new theorem, an adaption of hamminga's plausibility hypothesis is required because his hypothesis can only deal with theory developments directed to a proof of the same theorem. Instead of raising the plausibility of a theorem, I venture the new hypothesis that economists try to raise the plausibility of their theories. This is an enlargement of the old hypothesis because a theory is seen as a set of theorems proven with the same explanatory ideal. The old hypothesis is therefore a special case of this new hypothesis: raising the plausibility of a theorem means also raising the plausibility of the theory of which the theorem forms a part. The introduction of a new theorem can be seen as raising the plausibility of a theory. By proving more interesting theorems with the same explanatory ideal the plausibility of the theory is heightened.

Viewed this way Lancaster's theory of characteristics should be judged as more plausible than the Hicks and Allen theory: apart from proving their results under the same conditions, Lancaster is able to prove other interesting theorems concerning real life happenings, like the introduction of a new good, about which the Hicks and Allen theory has nothing to say. This situation is depicted in Figure 3.

By introducing characteristics as a new field dimension, the set of all conceptually possible worlds M is enlarged to M' because characteristics were implicitly assumed to be non variable in the old theory, can now take a variety of shapes. That is in Lancaster's terms: the consumption-technology matrix (denoting the relation between goods and their characteristics) was implicitly assumed to be diagonal. One of Lancaster's new theorems is the one that states that some goods can completely be displaced of the market as a consequence of the introduction of a new good. He proves this theorem for some non-diagonal consumption-technology so the elements of the corresponding set X are all lying outside the old set of conceptual possibilities M (see Figure 3). Moreover, he argues that the worlds in the extended part (M'- M) are much more plausible than the worlds in the old field M because he thinks it is obvious that all goods have certain set of characteristics and that it is because of this set of characteristics that the goods are valued. This idea is much more in congruence with common-sense than the old ideas.

It has be shown by now that the development strategies described in section two all lead to a raise in the plausibility of a theory, that is heightening the chance that it is true in the `real' world. Therefore these plausibility driven strategies are perfectly rational, having their own logic independently of empirical tests results. Moreover, it has been shown that the exact nature of the plausibility convictions of an economist (as represented by a plausibility function) does not influence his appreciation of a theory development. No matter the shape of his plausibility function, the development strategies described all lead to a raise of the plausibility of the theory. It is maybe for this reason that discussions about plausibility convictions are rarely found in economic literature, because it is not necessary to discuss these convictions to come to an agreement about considering a theory development as progressive or not. But although rarely discussed plausibility reasoning plays a crucial role in theory development in directing the line of research, as was shown also in this section. Question remains to be answered why theoretical economists have implicitly chosen to adopt this methodology instead of some other, more empirically based, method.

4. The relevance of econometric tests

In the falsificationist view on the practice of economists empirical investigation is used to test the implications, and maybe the assumptions, of a theory, which will, consequently, be adapted depending on the results of these tests. This ideal is held by most economists and has been fuelled in the past by the writings of economic methodologists. We have seen however that economic theory develops according to rules other than the rules of empirical testing. But surely there have been studies in which an attempt have been made to test the theory of consumer behaviour one can argue. Then, what explains the above noted fact that these studies have had no influence on the direction of theoretical research? Theorists are perfectly aware of the empirical studies conducted but they still hang on to the plausibility driven development strategies discussed above. This behaviour emanates not because of unwillingness to `listen' to empirical results but is a consequence of the way empirical research in economics is (necessarily) conducted, rendering it limited theoretical meaning.

Most empirical studies concerning consumer behaviour are applied demand analyses. Typically econometricians assume a Hicks and Allen utility maximization framework in order to specify a demand system and try next to estimate this system on fairly long time series of macro data of price and quantity indices of broadly defined groups of commodities. During the late 1960s and 1970s the results of such estimations were frequently used to test the theorems of consumer theory primarily the theorem of homogeneity of the demand functions and the symmetry of the substitution matrix. These tests turned out to be negative, especially homogeneity was frequently rejected. However, what was tested in this way were not the theorems of the Hicks and Allen theory. These theorems concern the behaviour of an individual consumer buying individual commodities. But the tests assumed utility maximizing which applies to a group of consumers spending money on several groups of commodities. To make possible this twofold aggregation of both consumers and commodities several very restrictive assumptions have to be added to the original Hicks and Allen theory (like separability of the utility function, equal income elasticities for the commodities belonging to one group etc.) Furthermore, econometricians have to rely on at least two more auxiliary assumptions: the assumption of a correct specification of the demand system and the assumption of an infinite size of the sample which is used to estimate the parameters of the system. Especially the last assumption turns out to be very crucial because econometricians have only small samples for their estimations, which results in tests being biased towards rejection.

Other tests of consumer theory which are explicitly directed to the testing of the assumptions of consumer theory encounter problems of a similar nature. Take for example the well known test of revealed preference theory by Koo (1963). He made use of the data collected by a consumers food panel of 215 families who kept their weekly expenses on food for a year. After dividing the year in 13 periods of 4 weeks it followed that less than 1 percent of the families showed completely consistent behaviour in the 13 periods, i.e. consistent according to Houthakker's strong axiom of revealed preference. Question is: what implications for the theory follow from these results? This question however is never discussed and for reasons philosophers of science have known since Duhem stated his so called irrefutability thesis. This thesis states that a single hypothesis can never be straightforwardly tested, but only together with other (auxiliary) hypotheses. Therefore disconfirming test results can always be attributed to violations of these auxiliary hypotheses. So empirical results loose their meaning for the theory under consideration. Demand analysts needed restrictive aggregation assumptions in order to specify a demand system and had to assume this specification to be correct. Furthermore, they had to rely on the assumption of an infinite sample size. Only after these assumptions were married to the theory, tests could be performed. Therefore one cannot call them tests of the Hicks and Allen theory, because some augmented version of the theory is tested.

And in the study of Koo auxiliary hypotheses have to be made e.g. about the motivation of the participants in the consumer data panel and for the defining of the common price of a good experienced by all families during a period of four weeks. More important are fundamental hypotheses like the constancy of the family's tastes and preferences during the year, and the availability of sufficient information for making a consistent choice, which have to be made. In their turn these hypotheses also cannot be tested separately (see also Caldwell (1982)).

When disconfirming test results can be excused for by (implicitly) pointing at Duhem's thesis it is perfectly rational for theorists to develop their theory not in reaction to empirical results but by using plausibility driven development strategies. These strategies are independent of empirical results and have their own rationale in raising the plausibility of a theory, as was shown in the previous section.

One could object to this by pointing at other sciences like physics and arguing that Duhem's irrefutability thesis is equally in force in these scientific disciplines, without making theory `empirical immune'. Obviously this is true but however, it does not seem to give the same severe problems as it does in economics. As pointed out by others (e.g Hausman (1992)) the problem with economics is that researchers are only able to specify in a vague, impressionistic way just what the auxiliary assumptions, which are needed to test a theory, amount to, in contrast to physicists.

Concluding one could say that the testing of theoretical results is problematic because of the mass of, only vaguely known, auxiliary assumptions which have to be made to be able to perform a test. Therefore the results of such tests contain little guidance for theory development. No wonder theorists use plausibility driven development strategies as a substitute for more empirically driven strategies.

5. Concluding remarks

Despite what economists might believe and some methodologists recommend, economic theory does not develop under the influence of results of empirical testing, but is directed by common-sense and introspective plausibility convictions. Theorists can excuse themselves for using this methodology by referring to Duhem's irrefutability thesis. This thesis states that a single hypothesis cannot be straightforwardly tested but only when other auxiliary assumptions are married to it, restricting the theoretical meaning of the empirical results. The plausibility driven development strategies which are followed instead have their own rationale, independent of empirical test results. These strategies raise the plausibility of a theory, by proving an old theorem for a new set of conditions, by extending the field in which a theorem was proven, or by the introduction and proof of a new theorem. Using these strategies, theorists are able to agree about theoretical progression without considering econometric and other empirical evidence. This is even the case when they differ in opinion about which propositions should be called plausible, and which should not. Especially this aspect makes their method extremely powerful. The specific nature of economic theory development was exemplified by a short survey of the developments in the neo-classical research programme concerning consumer behaviour. Other studies show that this pattern of theory development can be discerned in other theoretical research programmes as well (in the theory of international trade (hamminga (1983)) and the capital structure theory (Cools (1993) discussed in Timmer (1995)).

Further investigations should point out whether this pattern can be found in other economic research programmes as well. I claim that this kind of research is valuable to both methodologists and economists. For methodologists because they acquire an picture of just what economists do in practice, instead of what they claim to do. And for economists because a meta-theory based on this sort of research will give them insight in making explicitly clear what they are intuitively doing, and why they are doing it. By studying the history of economic thought in this way methodological discussions may become more detailed and empirical, and hence maybe less exciting to a general public. But the profit could consist of a more direct bearing on the concrete decisions and experiences in the day to day professional life of theoretical economists.

Those who still hold that empirical tests have, and should have, a decisive influence on economic theory development may again be disappointed by this paper because no traces of test results could be found in the development of the theory of the consumer behaviour. But the consolation this time is hoped to consist of an overview of the reasons just why economic theory is `empirically immune', and a clear display of the powerful self-contained logic of theoretical research in terms of plausibility.

Acknowledgements: I am grateful to Bert hamminga, Theo Kuipers and Eddy Szirmai for providing invaluable comments on this paper.

References

- Allen, R.G.D. (1936), "Professor Slutsky's theory of consumers' choice" in Review of  Economic Studies III, p.120-129.
- Barten, A.P. en V. Bhm (1982), "Consumer Theory" in K.J. Arrow en M.D. Intriligator (eds.), Handbook of Mathematical Economics Vol. II, Amsterdam.
- Blaug, M. (1980), The Methodology of Economics, Cambridge.
- Brown, A. en A. Deaton, (1972), "Models of Consumer Behaviour: A Survey" in The Economic Journal vol. 82, London.
- Caldwell, B. (1982), Beyond positivism, London.
- Chipman, J.S., L. Hurwicz, M.K. Richter en H.F. Sonnenschein (eds) (1971) Preferences, Utility and Demand, New York.
- Cools, K. (1993), Capital Structure Choice, Tilburg.
- Cools, K., B. hamminga, and T.A.F. Kuipers (1994) "Truth Approximation by Concretization in Capital Structure Theory" in B. hamminga and N.B. de Marchi (eds.) Idealization VI: Idealization in Economics, Poznan Studies in the Philosophy of Social Sciences and the Humanities, vol. 38, pp. 205-228, Amsterdam.
- Debreu, G. (1959), Theory of value: an axiomatic analysis of economic equilibrium, New York.
- hamminga, B. (1983), Neoclassical Theory Structure and Theory Development, Berlin.
- Hausman, D.M. (1992), The Inexact and Separate Science of Economics, Cambridge.
- Hicks, J.R. (1939), Value and Capital, Oxford.
- Hicks, J.R. and R.G.D. Allen (1934), "A reconsideration of the theory of value" in Economica vol. I, London.
- Houthakker, H.S. (1950), "Revealed Preference and the Utility Function" in Economica vol.XVII, London.
- Hurwicz, L. (1971), "On the problem of integrability of demand functions" in Chipman e.a. (1971).
- Hurwicz, L. en H. Uzawa (1971), "On the integrability of demand functions" in Chipman e.a. (1971).
- Keuzekamp, H.A. (1994) "What if an idealization is problematic? The case of the homogeneity condition in consumer demand" in B. hamminga and N.B. de Marchi (eds.) Idealization VI: Idealization in Economics, Poznan Studies in the Philosophy of Social Sciences and the Humanities, vol. 38, pp. 243-254, Amsterdam.
- Klamer, A. and D.N. McCloskey (1988), "Economics in the human conversation" in A. Klamer, D.N. McCloskey and R.M. Solow (eds.) The consequences of economic rhetoric, Cambridge.
- Koo, A.Y.C. (1963), "An Empirical Test of Revealed Preference Theory" in Econometrica, vol.30, oktober 1963, pp.646-64.
- Lancaster, K. (1966), " A new approach to consumer theory" in The Journal of Political Economy, vol. 74, reprinted in K. Lancaster (1991) Modern Consumer Theory, Aldershot.
- Mirowski, P. (1989), More Heat Than Light, Cambridge.
- Nooteboom, B. (1986), "Plausibility in Economics" in Economics and Philosophy 2 (2), October, pp. 197-224.
- Robbins, L. (1934), An essay on the nature and significance of economic theory, London.
- Samuelson, P.A. (1938a), "A Note on the Pure Theory of Consumer's Behaviour" in Economica vol. V, London.
- Samuelson, P.A. (1938b), "A Note on the Pure Theory of Consumer's Behaviour
- An Addendum" in Economica, vol. V, London.
- Samuelson, P.A. (1948), "Consumption theory in terms of revealed preference" in Economica vol.XV, London.
- Samuelson, P.A. (1950), "The Problem of Integrability in Utility Theory" in Economica vol.XVII, London.
- Samuelson, P.A. (1983), Foundations of Economic Analysis (second edition), Cambridge.
- Sonnenschein, H.F. (1971), "Demand theory without transitive preferences" in Chipman e.a. (1971).
- Stigler, G.J. (1950), "The Development of Utility Theory" in The Journal of Political Economy vol.LVIII, reprinted in A.N. Page (1968) (ed.) Utility Theory: a book of readings, New York.
- Timmer, M.P. (1994), Methodologie bij Economen. Een meta-theorie aangaande theoretisch en empirisch onderzoek rond consumentengedrag, working paper, Department of Philosophy, RUG/Groningen, July 1994.
- Uzawa, H. (1960), "Preference and rational choice in the theory of consumption" in K.J. Arrow, S. Karlin and P. Suppes (eds.) Mathematical Methods in the Social Sciences, Stanford.

PHiLES 0.1: Top of Page Menu