Bert hamminga Back to: Index: Teaching Docs hamminga, B. (1997) Informatie, Waarheid en Werkelijkheid,inhoudsopgave Go to: Previous Section; Next Section
Page title: 8. Semantiek: de leer van de betekenis der voegtekens
Semantiek betekent: de leer van de betekenis, en onze semantiek van de voegtekens uit de vorige paragraaf was duidelijk niet gehaaid genoeg. Voor een betere definitie van de voegtekens gaan wij nu het begrip "waarheid" in stelling brengen, een machtig kanon!
We gaan uit van de vooronderstelling van de klassieke logica, ook wel genoemd het Platonistische standpunt (Plato, keigave filosoof 500 v. Chr.), nl. dat er voor elke atomaire volzin precies twee mogelijkheden zijn: hij is waar of hij is onwaar. Dat spreekt helemaal niet vanzelf! Je zou ook kunnen kiezen voor bijvoorbeeld de indeling: waar/ onwaar/ onduidelijk. Neem bijvoorbeeld de atomaire zin: "het regent". Is die niet onduidelijk? Hij is waar als is bedoeld: "Het regent op maandag 5 januari 1987 in New York gedurende de ochtend" (daar zat ik toevallig koffie te drinken). Hij is onwaar als is bedoeld: "Het regent op dinsdagochtend 6 januari 1987 om 01.24 uur in Utrecht" (daar zit ik op dit moment dit dictaat te verbeteren).
"Het regent" kan een onduidelijke zin zijn, en dan is
het g��n volzin waarover wij het zullen hebben (maar een volzinsfunctie). Meestal
is "het regent" wel duidelijk, want mensen die dat zeggen bedoelen dan:
"Het regent op dit moment hier buiten", en de mensen die het te horen krijgen
weten dat. Soms is zo'n duidelijke volzin natuurlijk onwaar. Als een duidelijke volzin
niet onwaar is, is hij waar en omgekeerd. Als een zin iets anders is dan waar of onwaar
dan mag hij niet meedoen. Of, plechtig gezegd: dan is het geen volzin in de
betekenis die de klassieke logica aan dat woord geeft. Er zijn vele duidelijke volzinnen
waarvan we niet weten of ze waar zijn of niet ("Er is een grootste priemgetal"),
maar die mogen wel meedoen. Het zijn toch volzinnen.
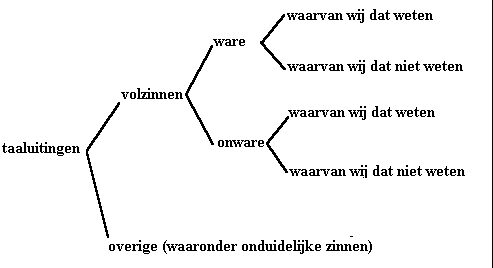
Dit schema geeft de zaak weer:

Nu gaan we, zoals dat heet, de formele taal van de propositielogica interpreteren, dat wil zeggen: uitleggen wat alle tekens die in die taal voorkomen betekenen. We gaan, nog anders gezegd, een semantiek opstellen voor de formele taal van de propositielogica. Een die beter is dan de taalkundige semantiek uit de vorige paragraaf. Net als in de vorige paragraaf kiezen we de letter P(P1, P2, Q, R, ... had ook gemogen) als afkorting voor een atomaire volzin. Dat zijn er natuurlijk oneindig veel. Er zijn bij invulling van een volzin voor "P" twee mogelijke resultaten: "P" is waar, zoals bij "Amsterdam is de hoofdstad van Nederland" en "P" is niet waar, zoals bij "3 < 1". In het eerste geval geven we "P" de waarheidswaarde 1, in het tweede geval geven we "P" de waarheidswaarde 0. Deze catalogus van twee mogelijkheden zetten we als volgt in een schema, en dat schema noemen we de waarheidstafel van de atomaire formule "P".
|
P |
I |
1 |
II |
0 |
Anders gezegd: atomaire volzinnen vallen in twee waarheidsgroepen uiteen: waarheidsgroep I, de ware atomaire volzinnen en waarheidsgroep II, de onware atomaire volzinnen.
De totale verzameling van volzinnen die uit twee atomaire volzinnen zijn samengesteld ("Het regent nu en het sneeuwt nu", "Als Pasen en Pinksteren op ��n dag vallen dan is twee plus twee vijf" etc. etc.) kan keurig worden opgedeeld in vier waarheidsgroepen van volzinnen, groep I, II, III, en IV in het volgende schema:
Voor twee atomaire formules "P" en "Q" zijn er in totaal 4 groepen van volzinnen:
| P | Q | ||
| I | 1 | 1 | (de groep volzinnen waarin P en Q beide waar zijn) |
| II | 1 | 0 | (de groep volzinnen waarin P waar is en Q niet) |
| III | 0 | 1 | (de groep volzinnen waarin Q waar is en P niet) |
| IV | 0 | 0 | (de groep volzinnen waarin P en Q beide onwaar zijn) |
Tabel 8.1.
Voor drie atomaire formules "P", "Q" en "R" zijn er in totaal acht groepen:
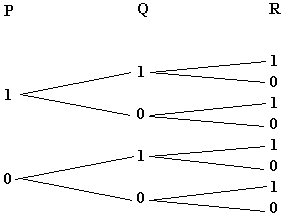
| P | Q | R | |
| I | 1 | 1 | 1 |
| II | 1 | 1 | 0 |
| III | 1 | 0 | 1 |
| IV | 1 | 0 | 0 |
| V | 0 | 1 | 1 |
| VI | 0 | 1 | 0 |
| VII | 0 | 0 | 1 |
| VIII | 0 | 0 | 0 |
Tabel 8.2.
Nu gaan we onze slag slaan: we gaan de betekenis van de symbolen "�", "�", "V", "&" en "�" defini�ren. Dat doen we door te laten zien hoe de waarheidswaarde (waarheid of onwaarheid) van de samengestelde volzinnen A � B, A � B, A V B, A & B en �A afhangt van de waarheidswaarde van de volzinnen A en B. De betekenis die wij nu kiezen voor de logische voegtekens kan nu afgelezen worden uit het volgende schema:
| A | B | A � B |
A � B |
A V B |
A & B |
A |
�A |
|
| I | 1 | 1 | 1 |
1 |
1 |
1 |
1 |
0 |
| II | 1 | 0 | 0 |
0 |
1 |
0 |
0 |
1 |
| III | 0 | 1 | 0 |
1 |
1 |
0 |
||
| IV | 0 | 0 | 1 |
1 |
0 |
0 |
Tabel 8.3.
Aldus besloten! Op deze betekenis van de voegtekens leggen we ons vast. Deze methode van vastleggen noemen we de logische semantiek voor de voegtekens van de formele taal voor de propositielogica.
We leggen ons vanaf nu beslist niet meer vast op de taalkundige semantiek, m.a.w. we leggen er ons dus niet meer op vast dat de symbolen altijd de volgende betekenis hebben:
:� all��n als ... dan ...
�: als ... dan ...
V: of
&: en
�: niet
Anders gezegd: als ergens een volzin "A of B" staat, dan mag je niet meer zomaar "of" vervangen door "V". Je moet eerst onderzoeken of de schrijver (spreker) "V" bedoelt als hij "of" zegt. Meestal is daar makkelijk achter te komen. En meestal is het ook zo.
We zeggen, nu h��l slim, dat de taalkundige semantiek vaak wel zal kloppen, maar dat de definites met behulp van de waarheidstafel voor formules A en B de absolute doorslag geven. Dus: voor de volzinnen A en B geldt krachtens de logische semantiek:
A � B is all��n waar wanneer A en B dezelfde waarheidswaarde (1 of 0) hebben (anders is A � B onwaar).
A � B is all��n onwaar als A waar is en B onwaar (anders is A � B waar)
A V B is all��n onwaar als A en B beide onwaar zijn (anders is A V B waar)
A & B is all��n waar als A waar is en B ook (anders is A & B onwaar)
�A is all��n waar als A onwaar is (anders is �A onwaar)
Omdat de waarheid van volzinnen A � B, A � B, A V B, A & B en �A in de nu gekozen semantiek afhangt van de waarheid van A en B, zoals de waarde van een wiskundige functie afhangt van de getallen die je erin stopt, noemen we "�", "�", "V", "&" en "�" nu ook wel waarheidsfuncties. En kunnen we dingen zeggen als (zie ook ' 6):
C = f (A, B) = A � B
Go to: Previous Section; Next Section