LINCONS(Y, C) := {(Y, C) | C = Y -17}

Zo iemand houdt bepaalde dingen voor mogelijk en andere voor onmogelijk. Combinaties (Y,C) die weergegeven worden door punten op de lijn in fig. 25.1. zijn volgens deze hypothese mogelijk, alle andere waarden die je voor (Y,C) mag invullen zijn volgens deze hypothese niet mogelijk. Deze waarden zullen volgens de hypothese in de werkelijkheid nooit gemeten worden. Dat is de informatie, in de preciese betekenis die dat woord in deze cursus heeft gekregen.

De hypothese zegt echter niets over causaliteit, over oorzaak en gevolg. Het kan zijn, en zo wordt gewoonlijk de consumptiefunctie geïnterpreteerd, dat de veranderingen in het nationaal inkomen de oorzaak zijn van veranderingen in de consumptie. Maar het kan ook zijn dat de causaliteit omgekeerd ligt: Veranderingen in de consumptie zouden dan leiden tot veranderingen in het nationaal inkomen. Als de consumptiefunctie de enige relatie zou zijn in een model zouden we hierin een keus moeten maken, die niet uit het bestaan van het relatie af te leiden is.

DEFINITIE:  Een variabele in een model die, als hij verandert van waarde, de verandering van de waarde van andere variabelen tot gevolg heeft, maar niet op zijn beurt door variabelen van het model wordt beinvloed heet een exogene variabele van dat model. Een variabele in een model waarvan de waarde verandert als gevolg van de verandering van de waarde van andere variabelen in het model heet een endogene variabele van dat model.

Neem het volgende model:

26.1. Y := C + I

26.1. C = a₁ Y + a₂

26.3. I = a₃ r + a₄

Er zijn 3 vergelijkingen en 8 variabelen. Y is het nationaal inkomen, C de nationale consumptie, I de nationale investeringen, r is de rentevoet. De overige variabelen (a₁, a₂, a₃, a₄) zijn niet direct meetbaar. Dit zijn dus de parameters van het model.

Er zijn dus 4 meetbare variabelen (Y, C, I, r).

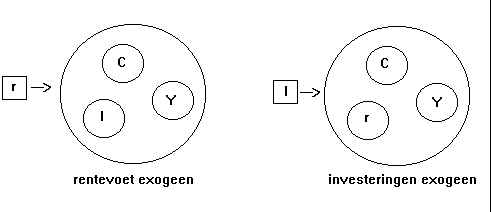
Daarvan kan ik er maar drie oplossen met behulp van de relaties uit het model. Ik moet dus nu een keuze maken; ik moet een hypothese invoeren over oorzaak en gevolg. Daarvoor zijn er in principe vier mogelijkheden. De volgende twee daarvan liggen het meest voor de hand.

Als ik kies voor de linker hypothese: (Y, C, I) worden bepaald door de waarde van de parameters en door de rentevoet, dan (Y, C, I) zijn dus nu mijn endogene variabelen geworden en r is mijn exogene variabele geworden. Maar waarom zou ik dat doen en niet voor de rechterhypothese kiezen?

Een voorstander voor een exogene rentevoet zou kunnen zeggen dat een hoge rente investeren afschrikt, en consumeren met geleend geld. Als de rente laag is, is investeren en consumeren met geleend geld goedkoop en dan neemt dat dus toe.

Een voorstander van exogene investeringen kan erop wijzen dat het optimisme over de toekomst, en niet de rente de investeringen van ondernemers bepaalt, en als ze dan optimistisch zijn dan gaan ze er geld voor lenen en dat drijft de rente op. Zijn ze pessimistisch dan willen ze hun geld niet investeren, maar liever uitlenen, bijv. aan een ander bedrijf of een bank. Als iedereen dat wil, gaat de rente omlaag.

Wil ik uiteindelijk voorspellingen met het model kunnen gaan doen dan moet ik weten wat het model voorspelt: Y,C en I op basis van r, of juist Y,C en r op basis van I. We kiezen eerst maar eens voor de eerste partij (linkerplaatje, r exogeen)

Voor een voorspelling is de volgende stap uit te zoeken welke de beste waarden zijn die ik kan invullen voor (a₁, ..., a₄) om zodoende van (26.1.) en (26.2.) (26.3.) specifieke relaties te maken.

In (26.1.) zit geen parameter omdat deze vergelijking slechts een definitie van de variabele Y is.

De gereduceerde vorm van het model is

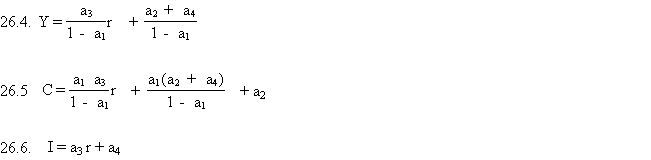
Als we geschatte waarden hebben voor (a₁, ..., a₄) kunnen we voorspellen wat de waarden van (Y, C, I) zullen zijn op basis van een bepaalde r. We moeten nog aan de goede waarde voor r zien te komen want die krijgen we niet uit het model, die moet er juist als gegeven in. Hoe lossen we dat op? Een deskundige vragen? Een twee model maken waarin r endogeen is? Welke exogenen laten we daarin toe? Y,C en I ook?

Stel dat ons het ook nog lukt buiten ons eigen model om een voorspelling van de rente te krijgen. De veranderingen van de rentevoet zullen, volgens ons model, leiden tot veranderingen van (Y, C, I). Maar als onze parameters (a₁, ..., a₄) zouden veranderen dan zou dit betekenen dat toekomstige waarden van (Y, C, I, r) niet meer zouden voldoen aan de door ons geschatte specifieke relatie. Dan kunnen we geen voorspelling meer doen.

Over de drie variabelen (Y, C, I) kunnen we, samenvattend  conditionele (aan voorwaarden gebonden) voorspellingen doen. Voor bijvoorbeeld Y ziet deze conditie er als volgt uit:

(1) Als vaste parameterwaarden (a₁^*, a₂^*, a₃^*, a₄^*) goede benaderingen van gemeten viertallen (Y, C, I, r) door het model opleveren en

(2) Als dit zo blijft en

(3) Als de rentevoet r^* wordt

Dan wordt Y gelijk aan

Als aan conditie (1) is voldaan hebben we een model dat het gedrag van de variabelen tot dusverre goed beschrijft. Deze conditie is evenwel niet voldoende voor wie een voorspelling wil doen. Wie dat wil doen moet vooronderstellen dat die variabelen zich in de toekomst netjes volgens de specifieke relaties van het kwantitatieve model blijven gedragen (conditie 2).

Ook dat blijkt tenslotte nog niet voldoende. Uit het kwantitatieve model valt niets af te leiden over wat er met de exogene variabelen zal gebeuren. En daar hangt alles vanaf! Geheel los van het model zal eerst een voorspelling moeten worden gedaan over het toekomstig verloop van de exogene variabelen, voordat met behulp van het model een voorspelling kan worden gedaan over het verloop van de endogene variabelen.