Bert hamminga Back to: Index: Teaching Docs hamminga, B. (1997) Informatie, Waarheid en Werkelijkheid,inhoudsopgave Go to: Previous Section; Next Section
Page title: 25. Generieke, specifieke en variabele relaties in de economie
Om het verschil uit te leggen tussen generieke, specifieke en variabele relaties in de economie beginnen we met een eenvoudig voorbeeld: de lineaire consumptiefunctie uit par. 23. De generieke relatie is in dit geval
DEFINITIE 25.1.
LINCONS(Y, C, a1, a2) := {(Y, C, a1, a2) | C = a1 Y + a2}.LINCONS is een verzameling van geordende 4-tallen uit
Â+ x Â+ x  x  .Er is een groot verschil tussen de variabelen (Y, C) en (a1, a2). Van de variabelen (Y, C) kunnen de waarden gemeten worden. Dit meten leverde (in par. 23.) geordende 3-tallen (j, Y, C) op die zich werkelijk hebben voorgedaan. De variabelen (a1,a2) daarentegen zijn niet direct meetbaar. Zij zijn geintroduceerd om de relatie tussen de meetbare variabelen Y en C een bepaalde vorm te geven (in dit geval de vorm van een rechte lijn). Een andere vorm had ook gekund, bijv.:
(Y, C, a1, a2):= {(Y, C, a1, a2) | C = a1Ya2}.Nu is het zo dat je bij elke gemeten waarde van (Y, C) wel een paar (a1, a2) kunt vinden waarvoor het waar is dat C = a1Y + a2.
Anders gezegd: de uitspraak
25.2.
" (Y,C) $(a1, a2) [C = a1 Y + a2]is waar krachtens de wiskunde, oftewel: is analytisch waar. Uitspraak 25.2. heeft geen inhoud. Zij geeft geen informatie.
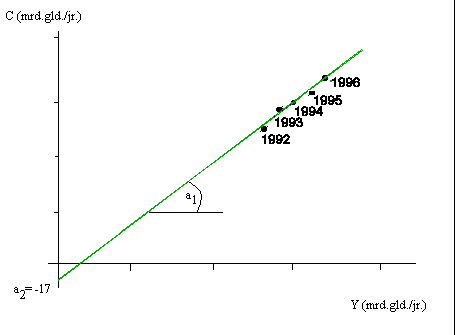
Als we voor (a1, a2) getallen hebben bijv. (1, -17) kunnen we een specifieke relatie opstellen. Dit is een verzameling van geordende twee(!)tallen (Y,C):
LINCONS(Y, C) := {(Y, C) | C = Y - 17}LINCONS (Y, C) is de verzameling van punten op de groene lijn in de volgende grafiek (figuur 25.1.)

Nu hebben we nog maar met twee variabelen te maken. De uitspraak
25.3.
" (Y, C) [C = Y - 17]is echter krachtens de wiskunde onwaar oftewel: is analytisch onwaar. Er zijn immers vele (Y, C)
ÎÂ+ x Â+ die niet aan de vergelijking C = Y - 17 voldoen. Zij worden voorgesteld door alle punten die in fig. 25.1. niet op de lijn liggen. de (specifieke) LINCONS(Y, C) de volgende hypothese opstellen:25.4.
" (j, Y, C) [(j, Y, C) Î OBS(j, Y, C) ® (Y, C) Î LINCONS(Y, C)]Hier staat: alle gemeten waarden voor (Y, C) zitten in de specifieke relatie
LINCONS(Y, C). Dit is een analytisch onbepaalde bewering. Deze bewering voldoet aan Poppers definitie (par19.1.) van empirische wetenschap. Er staat: van alle (j, Y, C)'s in OBS(j, Y, C) liggen de (Y, C)'s op de rechte lijn die LINCONS(Y, C) voorstelt. Deze uitspraak heeft inhoud (zie par 12): er zijn vele gevallen denkbaar waarin de uitspraak onwaar zou zijn. De inhoud, of informatie die 25.4. geeft is:25.5.
INFO(j, Y, C) := {(j, Y, C) | (j, Y, C) Î OBS(j, Y, C) & C ¹ Y-17}Wie de bewering 25.4. doet, zegt, met andere woorden
25.6.
INFO(j, Y, C) = Æen heeft ongelijk als er ook maar één element in deze verzameling blijkt te zitten. Dat kan heel goed gebeuren. Elk jaar komt er een (j, Y, C) bij op de website van het Centraal Bureau voor de Statistiek. De hypothese kan dus worden gefalsifiëerd.
In de economie wordt vaak de hypothese opgesteld dat de gemeten waarden der variabelen voldoen aan een willekeurige specifieke relatie, zoals C = a1 Y + a2 , waarbij men zich echter niet op voorhand vastlegt op de waarden van a1 en a2. Van deze waarden van (a1, a2) veronderstelt men dan dat ze niet in alle gevallen dezelfde zijn. Om zo'n soort hypothese op te schrijven hebben we het begrip "variabele relatie" nodig. In het voorbeeld van de consumptiefunctie is de variabele relatie:
DEFINITIE 25.4.
T(Y, C) := {(Y, C) | C = a1 Y + a2}T(Y, C) is (nog) geen verzameling van geordende tweetallen want we weten pas over welke verzameling van geordende tweetallen het gaat als we voor (a1
, a2) getallen hebben ingevuld.T(Y, C) is een variabele relatie waarvan we een relatie kunnen maken door bijv. voor (a
1, a2) in te vullen: (1, -17). We hebben dan de specifieke relatie LINCONS(Y, C) ingevuld voor T(Y, C).Zoals de variabele x een universum Ux heeft, zo heeft de variabele relatie
T(Y, C) een universum UT(Y,C). Ja, dat zie je goed, U is vet én cursief dus het is een verzameling van verzamelingen van verzamelingen van dingen.DEFINITIE 25.5.
UT(Y,C) = {T(Y, C) | (a1, a2) Î Â x Â}Als ik voor a1 en a2 reële getallen invul krijg ik elementen van de verzameling
UT(Y,C). Deze elementen zijn zelf specifieke relaties. LINCONS(Y, C) is daar één voorbeeld van.UT(Y,C) is de naam voor een familie van relaties. Voor een plaatje van de familie van relaties van het type LINCONS(Y, C) klik hier.Voor een plaatje van de familie van type QUADRCONS(Y, C) := klik hier.
Voor
LINCONS(Y, C) kan elke relatie in het universum UT(Y,C) worden voorgesteld door een rechte lijn in het eerste kwadrant van fig. 23.1. UT(Y,C) is dan de verzameling van al deze rechte lijnen.Economen nemen vaak een deel van deze lijnen als uitgangspunt bij hun redeneringen. Dan perken ze het universum dus in, bijvoorbeeld door de marginale consumptiequote tussen nul en een te houden:
DEFINITIE 25.6.
UT(Y,C) = {T(Y, C) | 0 < a1 < 1, a2 Î Â+}Vanuit dit voorbeeld komen wij nu tot een algemene formulering van de aard van deze drie typen van relaties en hun rol in de economie. We illustreren dit met het volgende fasenmodel:
: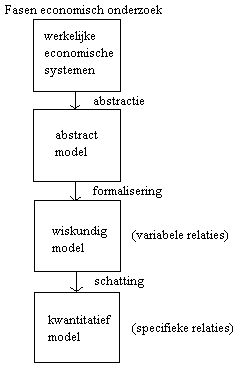
Uitgangspunt van theorievorming zijn economische systemen zoals die zich in werkelijkheid voordoen. Deze zijn echter zeer gecompliceerd. Onafzienbaar veel factoren beïnvloeden elkaar. In de eerste fase, die van de abstractie, worden de belangrijkste factoren voor het model geselecteerd en van de minder belangrijke wordt (eventueel: voorlopig) afgezien. In inleidende cursussen wordt vaak zeer drastisch geabstraheerd: men vooronderstelt bijvoorbeeld dat er geen overheid is, geen buitenland, dat er geen technische ontwikkeling is etc. Weliswaar worden zulke drastische abstracties in modellen die economen gebruiken meestal niet gemaakt, maar er blijven in elk model, hoe groot en gecompliceerd ook, altijd factoren buiten beschouwing. Men hoopt er dan op dat deze factoren geen belangrijke invloed hebben op de conclusies die men met behulp van het model over de werkelijke economie trekt.
In de tweede fase, die formalisering heet, worden de relaties tussen de geselecteerde factoren als wiskundige relaties geformuleerd, en wel als variabele relaties. Zo'n stelsel van variabele relaties heet een wiskundig model. Definitie 25.4. was een voorbeeld van zo'n variabele relatie. Het algemene geval van zo'n relatie, waarin er een willekeurig aantal (n) direct meetbare variabelen x1
Î Â, x2Î Â, ...xnÎ Â zijn en een willekeurig aantal (p) niet direct meetbare parameters a1Î Â, a2Î Â,..., apÎ Â), en er dus een willekeurige relatie is die elke denkbare vorm kunnen hebben, kun je toch nog met behulp van een impliciete functie f als formule opschrijven!:.DEFINITIE 25.7.
T(x1, x2, ..., xn) := {(x1, x2, ..., xn) | f (x1, ... ,xn, a1, ..., ap) = 0}In een derde fase worden voor de variabele relaties specifieke relaties ingevuld.
DEFINITIE 25.9. Een specifieke relatie S(x1, ... xn
) krijg ik door voor de parameters van een variabele relatie getallen in te vullen.Dat gaat zo: Uitgaande van een "data set", een verzameling waargenomen waarden OBS(x1, ... xn
) worden vaste getallen (a*1, a*2, ..., a*p) voor (a1, a2, ... ap) gezocht, zodanig dat "(x1, x2, ..., xn) [ (x1, x2, ..., xn)ÎOBS(x1, ... xn) ® f (x1, x2, ..., xn, a*1, a*2, ..., a*p) = 0 ]In de praktijk (zie figuur 23.1.) is niet mogelijk om door manipulatie van de waarden van (a1, a2,..., ap) de resulterende specifieke relatie zo te krijgen dat de punten wiskundig precies op de lijn liggen, en worden afwijkingen geaccepteerd binnen zekere grenzen die statistisch worden gedefinieerd. Een stelsel specifieke relaties dat op deze manier tot stand is gekomen heet een kwantitatief model.
Schatting levert vaak enorme problemen op, zoals in het geval van het (vis)marktmodel van voorbeeld 4 en 5 in par 23 . Wat zijn de getallen (a11*, a12*, a21*, a22*) voor parameters (a11, a12, a21, a22) waarmee de resulterende lijnen
D(p, x) = {(p, x) | x = a11 . p + a21}
S (p, x) = {(p, x) | x = a21 . p + a22}
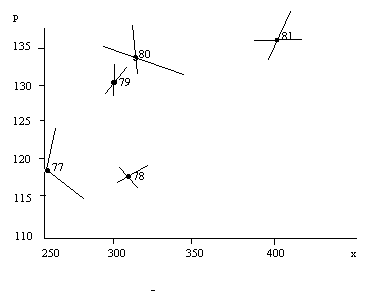
Het dichtste bij de waarnemingen uit OBS liggen? Het zou bijvoorbeeld gegaan kunnen zijn als in het onderstaande plaatje, die een comparatief statische theorie van evenwichtsverschuivingen weergeeft. Elke jaar veranderden de parameters, zodat het evenwicht telkens precies op de plek kwam te liggen van de waarneming van dat jaar. Dan is natuurlijk de vraag: door welke meetbare factoren werd dit veroorzaakt? Anders weten wij nog niets.
Een tweede mogelijkheid is gegeven in het volgende plaatje dat een dynamische theorie weergeeft van tijdpaden naar het evenwicht, eventulee verstoord door exogene schokken:
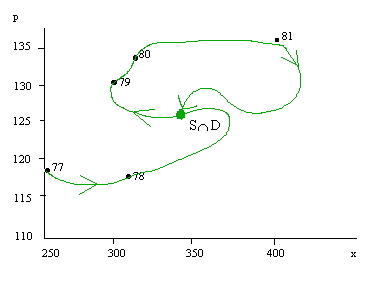
Dan luidt de theorie dat er maar één evenwicht is. Van 77 naar 78 was de markt op weg
naar het evenwicht, in 79 was hij ook eerst goed op weg, raakte hem zelfs vol, doch schoot
door naar punt 79, 80 en 81. Dit kan dan allemaal uit zichzelf zijn gegaan, zoals een
schommel doorzwaait als je hem scheef loslaat, of door schokken: iets of iemand heeft de
schommel op een bepaald moment een duw in een bepaalde richting gegeven.
Als er na 81 geen verstoringen meer op zouden treden, wat zeer onwaarschijnlijk is, dan
zou de markt uiteindelijk weer op het evenwicht komen.
Noch de comparatief statische, noch de dynamische theorie hebben veel waarde voor de mensen in de viswereld. Er moet meer kennis komen dan die in deze simpele voorbeelden beschikbaar is, wil iemand er iets aan hebben. De ellende is dat de dataset OBS geen enkele richtlijn biedt voor het benaderen van de a'tjes in
D(p, x) = {(p, x) | x = a11 . p + a21}
S (p, x) = {(p, x) | x = a21 . p + a22}
De parameters, zo heet dat, zijn niet identificeerbaar, de onderste fase van het fasenmodel is om wiskundige redenen onuitvoerbaar. Het mooiste dat je op zijn hoogst kunt bereiken is een speciaal geval, waarin de puntjes van OBS redelijk op een lijn of andere wiskundige functie liggen:
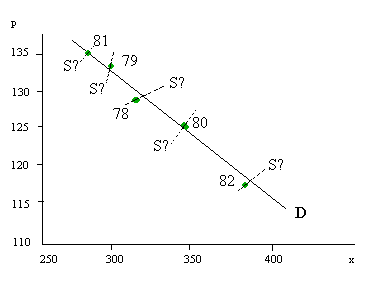
Wie gelooft in de theorie dat in deze jaren de vraagschaal D op zijn plek is gebleven, dus a11 en a12 bleven gelijk, en dat de aanbodparameters a21 en a22 telkens anders waren, kan a11 en a12 uitrekenen (maar a21 en a22 kunnen natuurlijk telkens oneindig veel verschillende combinaties van waarden hebben gehad, want er gaan nu eenmaal oneindig veel lijnen door een punt en als we maar één punt hebben, zoals bij S, dan weten we niet welke). In dit geval, dat zich helaas in de dataset OBS van de vismarkt niet voordeed, kan één van de twee lineaire relaties worden geschat.
Go to: Previous Section; Next Section