Verzamelingen, daar heb je twee soorten van: ongeordende en geordende. Bij ongeordende verzamelingen doet de volgorde waarin de dingen staan er niet toe. Neem bijv. U_x = Z. Als ik een ongeordende verzameling T van 10 getallen uit Z neem, dan ben ik niet geïnteresseerd in de volgorde. Ik kan zeggen:

22.1. Neem T := {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

en ik kan zeggen

22.2. Neem T := {0, 9, 1, 8, 2, 7, 3, 6, 4, 5}

Maar in 22.2. zeg ik precies hetzelfde als in 22.1. Ik wil gewoon die 10 getallen hebben en daarmee uit. Als ik ze maar alle 10 heb. Hoe kun je zien dat een verzameling ongeordend is? Dat kun je zien aan de accolades. Als de dingen uit de verzamelingen tussen "{" en "}" staan, is de verzameling ongeordend.

Een geordende verzameling dingen zetten we tussen "(" en ")". De volgende verzamelingen zijn allemaal verschillende verzamelingen:

22.3.

Oefening:

Reken zelf uit dat er 3.628.800 geordende verzamelingen (x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀) van 10 verschillende dingen uit T zijn (dus bijv.: (0, 0, 9, 8, 8, 7, 7, 1, 2, 3) telt niet mee). Doe het een keer met een calculator en een keer met potlood en papier (als dit laatste niet lukt, gebruik dan minstens een jaar geen calculator meer).

Nu kies ik de verzameling van dingen S_i, i = 1, 2, ..., 100 als mijn universum. Dus ik neem

22.4. U_Si:= {S₁, S₂, ..., S₁₀₀}

Net als in par 21 maak ik van U_Si een plaatje: de puntjes stellen de dingen in U_Si voor, de S_i's dus.

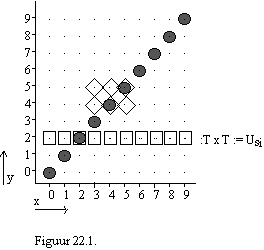
Het is een rooster. De rijen geef ik een naam met behulp van T (zie 22.1.). De kolommen ook. Het is dus een T x T - rooster. Daarom kunnen we U_Si ook "T x T" noemen. Zo'n soort afspraak gaan we straks maken.

Niemand kan het schelen in welke volgorde ik deze puntjes heb gezet:U_(x,y) := T x T is ongeordend. Maar elke S_i, i = 1, 2, ..., 100 is wel degelijk geordend. Voor het rooster heb ik de dingen uit T := {0, 1, 2, 3, 4, 8, 7, 9, 6} horizontaal en verticaal keurig volgens de Nederlandse telvolgorde gezet, maar dat was om de student een plezier te doen. Het was niet verplicht. Besef tenslotte nog: als in een geordend paar (x, y) geldt dat x = y, dan kun je de dingen in deze geordende verzameling omdraaien zonder dat ooit iemand er iets van ziet. Toch mag het niet! Dit geldt voor de puntjes met een rondje er om. Net als in alle universa kun je in  U_Si:= T x T verzamelingen definiëren. In zo'n verzameling zitten dan bijv. sommige S_i wel en andere S_i niet. De verzameling van alle punten met een rondje kan ik zo opschrijven:

22.5. S₁ (x, y) := {(x, y) | x = y} = {(0,0), (1,1), (2,2), (3,3), (4,4), (5,5), (6,6), (7,7), (8,8), (9,9)}

Nu de ruitjes:

En nu de vierkantjes:

22.7. S₃ (x, y) := {(x, y) | y = 2} = {(0,2), (1,2), (2,2), (3,2), (4,2), (5,2), (6,2), (7,2), (8,2), (9,2)}

Het rooster van Fig. 22.1. met de rondjes, ruitjes en vierkantjes die er

in staan, is een plaatje van het volgende model.

22.8. M₃ (x, y) :=(U_{(x, y)}, S₁ (x, y), S₂ (x, y),S₃ (x, y))

waarin

U_{(x, y)} := {S₁, S₂, .... , S₁₀₀}

S₁ (x, y):= {(0,0), (1,1), .... , (9,9)}

S₂ (x, y) := {(3,4), (3,5), .... , (5,5)}

S₃ (x, y):= {(0,2), (1,2), .... , (9,2)}

Fig. 22.1. is als weergave van deze M₃ (x, y) natuurlijk veel overzichterlijker, maar het gaat er om dat je de notatie begrijpt.

Wat hebben we van 22.1. t/m 22.8. gedaan? We hebben een verschrikkelijk moeilijke denkstap gezet met ons hoofd. Slordig uitgedrukt hebben we een tweede soort ding, y op de begane grond bij de x gezet en de hele zaak een etage hoger gemaakt. Kijk maar (figuur 22.2.):

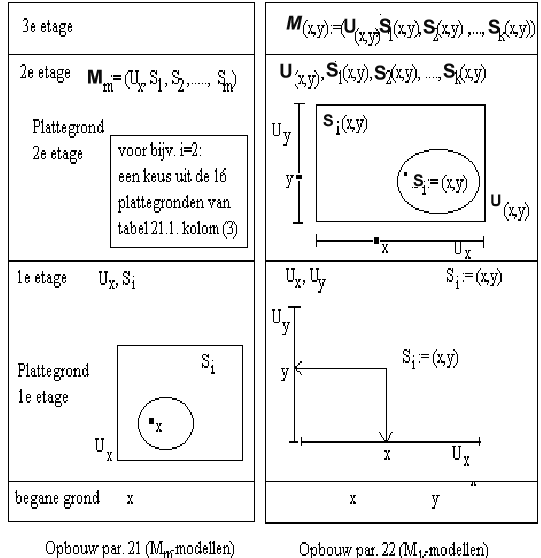
                                                            Fig 22.3

Op de eerste etage van de opbouw par 22 slaag ik er met enige kunst- en vliegwerk in om een (x, y), een geordende verzameling van twee dingen, als één punt voor te stellen. Dit lukt door U_x en U_y als lijnstukken voor te stellen. Een ding in U_x of U_y wordt nu voorgesteld door een punt op een lijnstuk, en niet meer, zoals in een Venn-diagram, als een punt in een vlak (zie linker plattegrond 1e etage). Daardoor kan ik een plattegrond van de 2e etage van de opbouw van par 22 maken die erg veel weg heeft van een Venn-diagram. Dit diagram noem ik een tweede orde Venn-diagram. De puntjes in deze rechthoek stellen verzamelingen van (twee) dingen voor. Bij een eerste orde Venn-diagram (een gewone), mag ik de puntjes door elkaar gooien. Bij een tweede orde Venn-diagram heeft het puntje van S_i een vaste plaats. Venn-diagrammen moeten ons helpen langs de kortst mogelijke weg de definities te begrijpen.

Wie goed heeft opgelet heeft gemerkt dat variabelen waar je dingen voor invult altijd kleine letters zijn: x,y,x₁ enz  Voor verzamelingen van dingen gebruiken we grote letters U_x, S,T,S₁ enz . Als we weer over verzamelingen van S'jes enz praten, gebruiken we vet: U_(x1,...,xn), S(x,y) enz. Dan komt vet cursief: M.

Daar komen ze (kijk elke keer naar figuur 22.2.suggestie: even de figuur uitprinten):

Beginnen we over verzamelingen te praten dan spreken we eerst af over welke verzameling U_x1  van dingen x₁, U_x2  van dingen x₂,....,U_xn  van dingen x_n we het hebben.  

S en T zijn verzamelingen van dingen (binnen een universum). Twee speciale soorten S'en en T's zijn definitie 22.1. en definitie 22.2.:

DEFINITIE 22.1.: (x, y):= een geordend paar:= de geordende verzameling bestaande uit eerst x en dan y.

DEFINITIE 22.2.: (x₁, x₂, ..., x_n):= een geordend n-tal (Engels: n-tuple):= de geordende verzameling bestaande uit eerst x_1, dan x₂ en dan ... en dan x_n.

DEFINITIE 22.3.:S(x, y):= een binaire (tweedimensionale) relatie:= een verzameling van geordende paren.

DEFINITIE 22.4.: S(x₁, x₂, ..., x_n):= een n-aire (n-dimensionale) relatie:= een verzameling van geordende n-tallen.

Bij twee van dergelijke verzamelingen zullen we deze aanduiden met S respectievelijk T. Zijn er meer dan twee, dan spreken we over S₁,S₂, .... ,S_k.

Voor de universa zijn geen nieuwe definities nodig: neem v:= (x, y) in definitie 21.2. Bedenk zelf dat U_(x,y) = U_xxU_y, in het algemeen:

U_{(x1,x2,...,,xn)}= U_x1xU_x2x...xU_xn

DEFINITIE 22.5.: U_x x U_y := (het cartesisch produkt) U_x maal U_y:= U_(x,y)

DEFINITIE 22.6.: U_x1 x U_x2 x ... x U_xn := (het cartesisch produkt U_x1 maal U_x2 maal ... maal U_xn := U_{(x1,x2,...,,xn)}

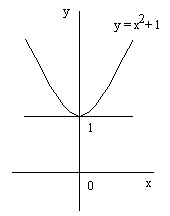
En inderdaad, voor S=(x,y) een verzameling geordende paren, geldt S=(x,y) Í Â x Â. Plechtig kan ik dus schrijven S=(x,y) = {(x, y) | y = x² + 1}

S(x₁, x₂, ..., x_n) := {(x₁, x₂, ..., x_n) | a₁ x₁ + a₂ x₂ + ... a_n x_n = 0}

Helaas! Tweede orde Venn-diagrammen zijn bij relaties bestaande uit geordende n-tallen, n > 2, niet meer te maken. Bij geordende 3-tallen kun je nog een bouwplaat maken of draden in een doorzichtige kunststof gieten. Daarna moeten wij puur met ons hoofd verder.

N.B. In een cartesisch-product-notatie staan de universa keurig op volgorde. U_{(x1,x2,...,,xn)} is echter geen geordende verzameling. Alléén de verzamelingen (x₁, x₂, ..., x_n) zélf zijn geordend.

We werken in deze paragraaf met speciale soorten verzamelingen, namelijk geordende verzamelingen (x, y) en (x₁, x₂, ..., x_n) en relaties S=(x,y) en S(x₁, x₂, ..., x_n). Dus zien de modellen er ook speciaal uit.

We herhalen eerst even:

DEFINITIE 21.7.: M_m := (U_x, S₁, S₂, ..., S_m).

Een model was een universum met een aantal verzamelingen waartoe de dingen uit het universum wel en niet kunnen behoren. We gaan, met onze kennis van geordende verzamelingen, de definities van M_m nog eerst verbeteren:

DEFINITIE 22.8.: M_m := (U_x, {S₁, S₂, ..., S_m}).

M_m is nu een geordend paar. De "x" is: U_x. De "y" is: {S₁, S₂, ..., S_m}. Dit

is een verbetering omdat het duidelijker weergeeft waarin we zijn genteresseerd: 1) Wat is het universum? 2) Wat zijn (de volgorde kan ons niet meer schelen!) de verzamelingen? Als we het antwoord op de vragen 1) en 2) weten, weten we over welk model het gaat.^*)

DEFINITIE 22.9.: M_k(x₁, x₂, ..., x_n) := een model met k relaties van geordende n-tallen (x₁, x₂, ..., x_n)

Toelichting: Nu volgt de meest uitgebreide beschrijving van een M_k(x₁, x₂, ..., x_n)

22.9. M_k(x₁, x₂, ..., x_n) :=(U_{(x1,x2,...,,xn}), {S₁(x₁, x₂, ..., x_n), S₂(x₁, x₂, ..., x_n), ..., S_k(x₁, x₂, ..., x_n)})

waarin

U_{(x1,x2,...,xn}) := {S₁, S₂, .... , S_m}

S₁, S₂, .... , S_m zijn geordende n-tallen (x₁,x₂,...,x_n)

S₁(x₁, x₂, ..., x_n) := {S_{1 1}, S_{1 2}, .... , S_{1 m1}}

S₂(x₁, x₂, ..., x_n) := {S_{2 1}, S_{2 2}, .... , S_{1 m2}}

........................................................

Net als kleding hebben modellen een maat. Die maat is (n, m, k, m₁, m₂, ...,m_k), n is het aantal dingen in elk geordend n-tal, m is the aantal geordende n-tallen in het universum, k is het aantal relaties. Elke relatie heeft, net als het universum, een bepaald aantal elementen; dus tenslotte zijn m₁, m₂, ..., m_k nog kengetallen van een model: een relatie kan veel elementen bevatten, maar een andere relatie kan bijv. weer leeg zijn.