Bert hamminga Back to: Index: Teaching Docs hamminga, B. (1997) Informatie, Waarheid en Werkelijkheid,inhoudsopgave Go to: Tabel Modeltypen (blad 1); Tabel Modeltypen (blad 2); Tabel Modeltypen (blad 3); Previous Section; Next Section
Page title: 21. Dingen
De meeste woordenboeken hebben er een hekel aan uit te leggen wat een "ding" is (zie
par 20, vraag 3, voorbeeld 3). Ik heb er ook niet veel zin in. Maar het moet.Wanneer weet ik of iets een ding is? Dat is niet moeilijk: als iets iets is, is het zeker een ding. Elk gespreksonderwerp is een ding, want zodra ik ergens iets over kan zeggen, kun je er donder op zeggen dat het een ding is. Er zijn in deze wereld alleen maar dingen. Andere dingen zijn er niet. Als ze er wel waren, waren het ook dingen. Trouwens, nu ze er niet zijn, zijn het ook dingen. Als je wilt laten zien wat een woord betekent, bijvoorbeeld "fiets", dan wijs je er een paar aan op het fietspad, en voor de zekerheid wijs je nog een paar auto's, bussen, motorfietsen en handkarren aan en vertelt dat dat geen "fietsen" zijn. Dit laatste is bij "dingen" onmogelijk, want je kunt niets aanwijzen dat géén ding is. Zelfs dingen die je niet kunt aanwijzen zijn dingen, dus als we die dingen zouden kunnen aanwijzen waren we nog niets opgeschoten: alles is een ding, zelfs wat niet bestaat.
Dat klinkt misschien erg raadselachtig, maar toch is het zo. Neem als voorbeeld een doorzichtig gebouw, genaamd "Sphereum", in de vorm van een halve bol met een diameter van 0,1 km. Dat is toch zeker een ding? Ik kan zelfs uitrekenen dat het Sphereum, als zijn rechte vlak op de grond staat, 50 m hoog moet zijn. Het is een ding, maar het ding bestaat niet (tenminste niet dat ik weet).
In mijn kleine uitleg over het Sphereum spelen drie dingen een rol. Ten eerste: het teken "Sphereum" als zwart patroon, zichtbaar op wit papier, of als patroon van geluidsgolven die in het menselijk oor een specifieke klankervaring teweeg brengen. Ten tweede het beeld van het Sphereum, een beeld dat door mijn beschrijving in iemands hoofd ontstaat. Ik was mijn bedoeling dat met mijn beschrijving een bepaald beeld is ontstaan. Als je wilt controleren of dat gelukt is, klik dan hier. Ten derde het object zelf, maar dat is er in dit geval niet. Door een of ander teken x te geven kan ik bij iemand een beeld oproepen. Zo'n beeld kan een object hebben. Als we denken dat dat zo is zeggen we "x bestaat" of "er zijn x'en". Als zo'n beeld geen object heeft zeggen we "x bestaat niet" of "er zijn geen x'en". De Maan bestaat, er zijn manen. Het Sphereum bestaat niet, er zijn geen Sphereums. Bij sommige dingen is het een hele klus om precies te bepalen wat het beeld is (haat, het getal 3, het voegwoord "en"). Als je weet wat iets is, dan kun je zeggen dat je een beeld hebt. Zoiets kan dus heel goed niet bestaan, ook al bestaat het beeld dan dus wel.
Het zijn allemaal dingen: manen, Sphereums, getallen, logische voegwoorden. Alles wat een naam heeft is een ding. Er zijn zelfs dingen die (nog) geen naam hebben.
Het meest eenvoudige dat mensen in talen over dingen zeggen is dat ze tot bepaalde verzamelingen behoren.
Voorbeelden:
1. Het Sphereum is een gebouw.
2. De Maan is een hemellichaam.
3. "en" is een logisch voegwoord.
Dit zijn volzinnen. Ze zijn propositielogisch onbepaald. Het zijn atomaire proposities. We gaan nu verder kijken dan de propositielogica: we gaan de atomaire propositie ontleden. Deze volzinnen zijn alle van de vorm
21.1. x Î S
waarbij voor x een ding is ingevuld en voor S een verzameling van dingen. "xÎS" is een volzinsfunctie (tenzij de letters x en S gereserveerd zouden zijn als namen van resp. een bepaald ding en een verzameling van dingen). De volzinsfunctie is een schema voor alle volzinnen die zeggen dat een bepaald ding tot een bepaalde verzameling behoort. Van "xÎS" kan ik een volzin maken door voor x en S iets in te vullen. De letters "x" en "S" stellen dus variabelen voor, waarvoor je bepaalde dingen mag invullen.
DEFINITIE 21.1. Het universum van de variabele v, (notatie: Uv) is de verzameling van dingen die je voor v mag invullen.
Voorbeeld: Stel we gebruiken de variabelen x en S, en Ux , het universum van x, is de verzameling van lichamen met een massa. Voor S mag je bepaalde verzamelingen invullen: US bestaat uit alle verzamelingen van lichamen met een massa.
| Vul je in: | Dan wordt "xÎS" |
| x: het Sphereum S: de verzameling van gebouwen |
een ware volzin |
| x: de Maan S: de verzameling van gebouwen |
een onware volzin |
Tabel 21.1.
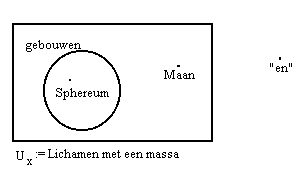
Het volgende plaatje heet een Venn-diagram:

Ux is een verzameling die ik als een rechthoek voorstel. Elk punt stelt een ding voor dat ik mag invullen van x. De maan en het Sphereum worden beide door zo'n punt voorgesteld. Het voegwoord "en" hoort niet bij Ux dus je mag het niet voor x invullen. De punt die het Sphereum voorstelt ligt in een rondje waarop en waarbinnen alle punten gebouwen voorstellen, en waarbuiten geen enkel punt een gebouw voorstelt. De twee invullingen geven:

We gaan in het vervolg de symbolen x, y, x1, x2, ..., xn , y1 , y2 , ..., yn gebruiken als variabelen waarvoor je dingen mag invullen. Meestal mag je niet zomaar dingen invullen. We zullen elke keer zo nodig het universum vastleggen van elke variabele die we gebruiken. We gaan de symbolen S, T, S1, S2,..., Sm, T1, T2, ..., Tm gebruiken als variabelen waarvoor je verzamelingen van dingen mag invullen. Verzamelingen zijn zelf natuurlijk ook dingen, dus het kan voorkomen dat je voor bijvoorbeeld "x" of "y" een verzameling mag invullen. Deze symbolen zijn nieuwe woorden. We moeten ook nieuwe zinnen afspreken:
DEFINITIE 21.2.: x
ÎS := x is een element van de verzameling S := x behoort tot S.DEFINITIE 21.3.: x
Ï S := x is geen element van de verzameling S := ¬(xÎS).DEFINITIE 21.4.: {x1, x2, ..., xn } := de verzameling bestaande uit x1, x2,..., xn.
DEFINITIE 21.5.: {x
| P(x)} := de verzameling van dingen die voldoen aan de eis P.| i = 1, 2, ..., n}". Zo'n eis P hoeft dus niet erg diepzinnig te zijn. Maar het kan: {x | x is een mens die verzameling-theorie moeiteloos toepast}. Let op: {x | P(x)} en {y | P(y)} en {x1 | P(x1)} en {x2 | P(x2)} en ... en {xn | P(xn)} betekenen allemaal precies hetzelfde (als de universa van x, y, x1, x2, en xn dezelfde zijn. Het doet er niet toe of je bij definitie 21.15. x, y, x1, x2, ..., xn-1 of xn gebruikt. De variabele x is hier, zo heet dat, een dummy (een "dommertje", hij hoeft nl. niets te doen).Toelichting: Op grond van definitie 21.5. mag ik in plaats van "{x1, x2, ...xn}" zeggen: "{xi
Als voor de dingen x uit Ux twee verzamelingen S en T zijn gedefinieerd, waar de dingen x wel of niet in kunnen zitten, dan zijn er de volgende mogelijkheden (dit is gewoon de waarheidstafel van P en Q)
| P: = xÎS | Q: = xÎT | |
| I | 1 | 1 |
| II | 1 | 0 |
| III | 0 | 1 |
| IV | 0 | 0 |
TABEL 21.2.
Deze mogelijkheden kunnen we ook afbeelden in een plaatje van Ux , een Venn-diagram:
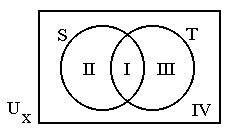
Ik neem aan dat ik aan een x duidelijk kan zien tot welk geval hij behoort. Er zijn geen twijfelgevallen. Ik kan de x'en dus sorteren in I'tjes, II'tjes, III'tjes en IV'tjes. S bestaat uit alle I'tjes en II'tjes. Ik trek er een rondje omheen. Binnen het rondje zitten alle x
ÎS. Ik trek ook een rondje om alle I'tjes en III'tjes. Dit zijn alle x'en in T.DEFINITIE 21.6.: S
Ç T := de doorsnede van S en T := {x | xÎS & xÎT}DEFINITIE 21.7.: S \ T := S zonder T := {x
| xÎS & x Ï T}DEFINITIE 21.8.: S
È T := de vereniging van S en T := {x | xÎS V xÎT}DEFINITIE 21.9.:
Illustraties:
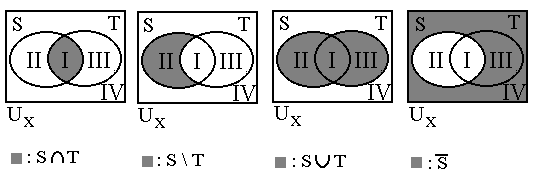
De volgende definities zijn alléén om het snel te leren:
Hulpdefinitie I: een I'tje := een x
ÎS 1 THulpdefinitie II: een II'tje := een x
ÎS \ THulpdefinitie III: een III'tje := een x
ÎT \ SHulpdefinitie IV: een IV'tje := een x
ÎIllustratie van Hulpdefinitie I en II: zie S
Ç T en S \ TIllustratie van Hulpdefinitie III en IV:
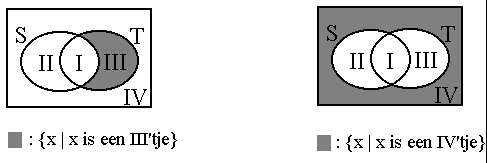
DEFINITIE 21.10.: Æ := de lege verzameling := Ux \ Ux
De illustratie van
Æ is wat vreemd: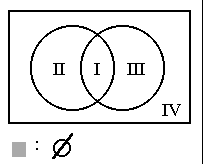
Er zit dus niet één x in Æ, want er is niets gearceerd. Als we willen zeggen dat er in een verzameling niets zit, kunnen we zeggen dat er hetzelfde in zit als in Æ.
Oefening: Er zijn nog 7 mogelijke deelvlakjes niet behandeld. Geef voor elk van hen de verzamelingtheoretische formule.
Zo. Breng nu maar universum Ux1 binnen, sorteer de x1'en uit in I'tjes, II'tjes, III'tjes en IV'tjes, trek er kringetjes om, en neem Ux2, doe hetzelfde met de x2 'en, enzovoort, tot alle dingen zijn gesorteerd. Zo ruim je je hoofd op!
DEFINITIE 21.11.: Mm := een model := (Ux, S1, S2, ..., Sm).
Toelichting: Deze definitie gaan we later nog verbeteren! M is in ieder geval een universum met een aantal verzamelingen waartoe de dingen in Ux wel en niet kunnen behoren. Wij houden het in het nu volgende simpel bij twee verzamelingen S en T, dus bij:
DEFINITIE 21.12.: M2 := (Ux, S, T).
"M" is beslist geen naam voor iets nieuws. Het is een naam voor dingen waarvan iedereen er al onvoorstelbaar veel in zijn hoofd heeft. Die dingen noemen we vanaf nu "modellen".
Voorbeelden van modellen die iedere deelnemer aan deze cursus al lang in zijn hoofd heeft, volgen nu in tabel Modeltypen (blad 1.).(Suggestie: open nu een nieuw venster klik hier voor een kopie van onderstaande tabel, om naar te kunnen blijven kijken of uit te printen).
(1) Model- type |
(2) Ontbre kende soorten |
(3) . Aanwezige soorten |
(4) | (5) | (6) |
Voorbeelden |
|||||
| Ux | S | T | |||
M2(0) |
I II III IV |
|
Sphereumobjecten  \ |
Van baksteen {x | x2 = 4} |
Met een toren {2} |
| M2(1) | II III IV |  |
Sphereumbeelden  |
Doorzichtig {x | x .0= 0} |
Vorm van een halve bol {x | x + 0 = x} |
| M2(2) | I III IV |  |
Zwaanobjecten  |
Met veren  |
Roze gespikkeld) {x | x > 1, x < 0} |
| M2(3) | I II IV |  |
Zwaanobjecten  |
Roze gespikkeld {x | x > 1 & x < 0} |
Met veren  |
| M2(4) | I II III |  |
Mausoleumobjecten  |
Nucleair aangedreven M's {x | x > 1 & x < 0, xÎÂ} |
M's in baan om aarde {x | x2 < 0, xÎÂ} |
| M2(5) | III IV |  |
Mensen (objecten) Â |
{x | x is mnl of vrl} {x | x . 0 = 0} |
Mensen met werk {x | x is even} |
| M2(6) | II IV |
|
Mensen (objecten) Â |
Mensen met werk {x | x is even} |
{x | x is mnl of vrl} {x | x = y + 1, yÎÂ} |
| M2(7) | II III | 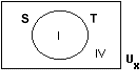 |
Dingen  |
Verzamelingen {x | x / 2 Î Z} |
Collecties {x | (x - 1) Ï Z} |
| M2(8) | I IV | 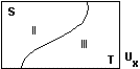 |
Mensen  \ {0} |
Mannelijke mensen {x | x is even} |
Vrouwelijke mensen {x | x is oneven} |
| M2(9) | I III | 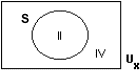 |
Mensen  |
Arbeiders {x | x is even} |
Die niet hoeven te eten {x | x > 0 en x < 0} |
| M2(10) | I II | 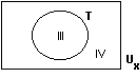 |
Mensen  |
Die niet hoeven te eten {x | x > 0 en x < 0} |
Arbeiders {x | x is even} |
| M2(11) | IV | 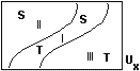 |
Inkomenstrekkers  |
Met een uitkering {x | x > -10} |
Die loon of rente ontvangen \{x | x < 10} |
| M2(12) | III | 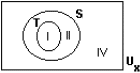 |
Volzinnen  |
Propositielogisch onware {x | x > 0} |
Die ik geloof {7} |
| M2(13) | II | 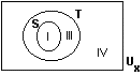 |
Volzinnen  |
Die ik geloof {7} |
Propositielogisch onware {x | x > 0} |
| M2(14) | I |  |
Volzinnen  |
Analytisch waar {x | x < -1} |
Analytisch onwaar {x | x > 1} |
| M2(15) | geen | 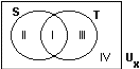 |
Vogels  |
Zwanen {x | 10 < x < 20} |
Witte {x | 15 < x < 25} |
Onder: Tabel Modeltypen (blad 2)
Onder: Tabel Modeltypen (blad 3)
(Suggestie: open nu een nieuw venster klik hier voor een kopie van onderstaande tabel, om naar te kunnen blijven kijken of uit te printen)
(1) Model- type |
(2) Ontbre kende soor ten |
(3) Aanwezige soorten |
(11) S |
(12) "x (xÎT®xÎS) =: S É T |
(13) SÊT & S¹T =:SÉT |
(14) "x (xÎS®xÎT) . =: S Í T |
(15) SÍT & S¹T =:SÌT |
(16) "x (xÎS®xÏT) . S Ç T = Æ |
M2(0) |
I II III IV |
|
0 |
1 |
0 |
1 |
0 |
1 |
| M2(1) | II III IV |  |
0 |
1 |
0 |
1 |
0 |
0 |
| M2(2) | I III IV |  |
0 |
1 |
1 |
0 |
0 |
1 |
| M2(3) | I II IV |  |
0 |
0 |
0 |
1 |
1 |
1 |
| M2(4) | I II III |  |
0 |
1 |
0 |
1 |
0 |
1 |
| M2(5) | III IV |  |
0 |
1 |
1 |
0 |
0 |
0 |
| M2(6) | II IV |
|
0 |
0 |
0 |
1 |
1 |
0 |
| M2(7) | II III |  |
0 |
1 |
0 |
1 |
0 |
0 |
| M2(8) | I IV |  |
0 |
0 |
0 |
0 |
0 |
1 |
| M2(9) | I III |  |
0 |
1 |
1 |
0 |
0 |
1 |
| M2(10) | I II |  |
0 |
0 |
0 |
1 |
1 |
1 |
| M2(11) | IV |  |
1 |
0 |
0 |
0 |
0 |
0 |
| M2(12) | III |  |
0 |
1 |
1 |
0 |
0 |
0 |
| M2(13) | II |  |
0 |
0 |
0 |
1 |
1 |
0 |
| M2(14) | I |  |
0 |
0 |
0 |
0 |
0 |
1 |
| M2(15) | geen |  |
1 |
0 |
0 |
0 |
0 |
0 |
Wij hebben oneindig veel van deze simpele M2's in ons hoofd. En de meeste van deze M2's zijn al redelijk netjes opgeruimd. Wie een voldoende haalt voor een bepaald tentamen, heeft ongetwijfeld redelijk begrepen over welke xi'en de tentamenstof ging en heeft ze ook merendeels juist uitgesorteerd met behulp van S'en en T's in I'tjes, II'tjes, III'tjes en IV'tjes.
Wie niet wist dat dat zo ging hoeft nu niet te schrikken: kinderen bijvoorbeeld kunnen ook al jaren spreken voor ze grammatica begrijpen. Wij zijn gewoon zo geconstrueerd, maar: wij kunnen onze eigen constructie leren begrijpen.
Ondertussen zijn er niet in elke M2 I'tjes en II'tjes en III'tjes en IV'tjes te vinden. Er zijn 16 mogelijkheden, d.w.z. 16 Modeltypes, aangeduid als M2(0) t/m M2(15) in tabel 21.2. In kolom (2) staat welke soorten (I'tjes, II'tjes, III'tjes en IV'tjes) ontbreken.
OPDRACHT: Ga zelf na dat er niet méér dan 16 mogelijkheden zijn.
De 32 modellen van tabel Modeltypen (blad 1) zijn keurig gerangschikt naar modeltype. We hebben van elk type twee voorbeelden in een Venn-diagram in kolom (3).
Opdracht: Bekijk achtereenvolgens de modeltypen M2(0) t/m M2(15). Doe het zo:
1) Bedenk dat S de vereniging is van I'tjes en II'tjes, en dat T de vereniging is van I'tjes en III'tjes;
2) Bekijk bij een modeltype welke soorten (I'tjes, II'tjes, III'tjes en IV'tjes) ontbreken (tabel 21.2., kolom 2 en 3);
3) Kijk en begrijp het Venn-diagram van dit modeltype;
4) Lees de voorbeelden van dit modeltype in Modeltypen (blad 1), en begrijp dat het echt voorbeelden van dit modeltype zijn;
5) Verzin zelf nog twee voorbeelden (niet beide uit de wiskunde);
6) Neem het volgende modeltype en doe hetzelfde.
WAARSCHUWING:
Dit kost heel veel tijd, maar het is belangrijk!
S en T mogen nooit (half) buiten Ux liggen. Deze
vetgedrukte (Ux, S, T):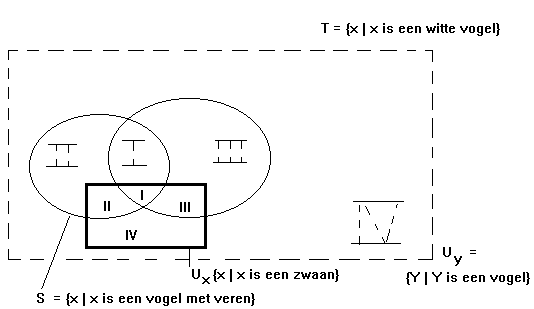
is in ons spel verboden. Ik mag mijn Ux zo groot en klein kiezen als ik wil, maar mijn S en T mag ik nooit "groter" kiezen dan mijn Ux. Wie ook over andere dingen dan zwanen wil praten moet een groter gespreksonderwerp kiezen, bijvoorbeeld Uy = {y | y is een vogel}.
We definiëren voor de handigheid nog twee afkortingen van zinnen:
DEFINITIE 21.13.:
" x(xÎS) := alle dingen (x'en) in Ux voldoen aan eis P.DEFINITIE 21.14.:
$x(xÎS) := er is tenminste een ding (x) in Ux dat voldoet aan eis P:= ¬" x(¬P(x)).Toelichting: "
"" en " " noemen we kwantoren. " x(¬(xÎS)) betekent dus ook hetzelfde als ¬$ x(xÎS).We kunnen nu bijv. schrijven
in plaats van "er zijn I'tjes":
$x(xÎS Ç T) enin plaats van "er zijn geen I'tjes":
" x(x Ï S Ç T) enin plaats van "er zijn II'tjes":
$x(xÎS \ T) enin plaats van "er zijn geen II'tjes":
"x(x Ï S \ T) enin plaats van "er zijn III'tjes":
$x(xÎT \ S) enin plaats van "er zijn geen III'tjes":
" x(x Ï T \ S) enin plaats van "er zijn IV'tjes": x(x
Îin plaats van "er zijn geen IV'tjes": "x(x
ÏErg nuttig is dit niet: het is immers nauwelijks korter. Maar het kan en het ziet er reuze gewichtig uit! (En het is een goede oefening; zorg dus dat je het begrijpt.)
Uit definitie 21.13. en definitie 21.14. blijkt ook dat
De formule |
Hetzelfde betekent als |
$x(xÎS) |
¬"x(¬(xÎS)) |
$x(¬(xÎS)) |
¬"x(xÎS) |
¬$x(xÎS) |
"x(¬(xÎS)) |
¬$x(¬(xÎS)) |
"x(xÎS) |
N.B. Uit
"x(xÎS) volgt niet $x(xÎS), want Ux kan leeg zijn! Dit is een afspraak over M2 (0): in M2(0) zullen we volhouden dat $x(xÎS) altijd onwaar is, voor elke S, want er is immers niets in Ux, maar "x(xÎS) is waar! Een beetje vreemd misschien, maar andere afspraken zouden nog veel vreemder zijn. Je kunt het beste onthouden dat $x(xÎS) betekent dat er een x is, en "x(xÎS) zegt alleen maar dat er geen III'tjes en IV'tjes zijn, en dat is ook waar als er helemaal niets is!. Herinner je je nog van toen ze je uitlegden dat 0*10 000 = 0 en 1/0 bestaat niet. Dat was ook wat gek, maar wel de beste afspraak die je kunt maken. "Æ" is onze nul, om zo te zeggen.Merk het volgende op: bijv. Ux =
 kun je van de volzinsfunctie "xÎS" een volzin maken door voor zowel x als S iets uit  in te vullen (bijvoorbeeld: x: = Ö2 en S := À, natuurlijke getallen, maakt xÎS onwaar). Wil je van de volzinsfunctie ""x(xÎS)" een volzin maken dan hoef je alléén voor S iets in te vullen (Bijvoorbeeld: "x(x = x) is waar en "x(x is even) is onwaar). Voor de variabele x wordt niets ingevuld en toch krijg je een volzin! We zeggen dat de variabele gebonden is door de kwantor """.Wat is de betekenis, oftewel de informatie die we geven als we over de relatie tussen twee verzamelingen S en T in een model M := (Ux, S, T) iets beweren? We kunnen we de betekenis van zo'n bewering bepalen door vast te leggen welke modeltypen ((M2(0) t/m M2 (15)) door de bewering worden uitgesloten. Net altijd is ook hier de informatie weer datgene wat volgens de bewering niet kan. We gaan nu een aantal relaties tussen S en T, gewoonlijk weergegeven door "=", "
¹", "Ê", "É", "Í" en "Ì", definiren door precies vast te leggen welke modeltypen door de bewering dat een dergelijke relatie tussen S en T bestaat, worden uitgesloten. (In beweringen waarin "Î" met logische voegtekens voorkomt, heeft "Î" altijd voorrang, spreken we af).DEFINITIE 21.15. S = T := S is T :=
" x(xÎS « xÎT)Toelichting: in par 8 hebben we gedefinieerd:
| P | Q | P«Q | |
| I | 1 | 1 | 1 |
| II | 1 | 0 | 0 |
| III | 0 | 1 | 0 |
| IV | 0 | 0 | 1 |
Tabel 21.4.
Dat blijft zo als we voor P nemen: x
ÎS en voor Q: xÎT.Dus zegt definitie 21.15.: alle x'en zijn I'tjes of IV'tjes; er zijn in ieder geval geen II'tjes en III'tjes zoals je kunt zien in de modellen van modeltype M2(7). Maar misschien ontbreekt er méér. Want als alle x'en en I'tjes zijn zoals in modellen van type M2(1), is ook voldaan aan
" x(xÎS«xÎT). En als alle x'en en IV'tjes zijn zoals in modellen van type M2(4) ook. En, een beetje raar misschien, maar toch: als er helemaal geen x'en zijn in Ux zoals in modellen van type M2(0) dan klopt het ook.Eigenlijk zegt S = T dus:
De M waar we over praten is van type M2(0), M2(1), M2(4) of M2(7).
en de overige mogelijkheden voor M zijn uitgesloten, want dat zijn allemaal modeltypen met II'tjes of III'tjes of allebei.
Ik kan dus de katalogus van 16 mogelijke modeltypes zien als een waarheidstafel met 16 rijen, en een waarheidskolom van S = T maken door enen te zetten bij M2(0), M2(1), M2(4) en M2(7), en bij de andere modeltypen nullen.
Dit heb ik gedaan in kolom 7 van Tabel Modeltypen (blad 2)
(Suggestie: open nu een nieuw venster klik hier voor een kopie van onderstaande tabel, om naar te kunnen blijven kijken of uit te printen)
Tabel Modeltypen (blad 2)
(1) Model- type |
(2) Ontbrekende soorten |
(3) Aanwezige soorten |
(7) "x (xÎS«xÎT) =: S = T |
(8) ¬ ( S = T) =: S ¹ T |
(9) "x(xÎS«xÏT) =: S = T |
(10) . Ux = Æ |
M2(0) |
I II III IV |
|
1 |
0 |
1 |
1 |
| M2(1) | II III IV |  |
1 |
0 |
0 |
0 |
| M2(2) | I III IV |  |
0 |
1 |
1 |
0 |
| M2(3) | I II IV |  |
0 |
1 |
1 |
0 |
| M2(4) | I II III |  |
1 |
0 |
0 |
0 |
| M2(5) | III IV |  |
0 |
1 |
0 |
0 |
| M2(6) | II IV |
|
0 |
1 |
0 |
0 |
| M2(7) | II III |  |
1 |
0 |
0 |
0 |
| M2(8) | I IV |  |
0 |
1 |
1 |
0 |
| M2(9) | I III |  |
0 |
1 |
0 |
0 |
| M2(10) | I II |  |
0 |
1 |
0 |
0 |
| M2(11) | IV |  |
0 |
1 |
0 |
0 |
| M2(12) | III |  |
0 |
1 |
0 |
0 |
| M2(13) | II |  |
0 |
1 |
0 |
0 |
| M2(14) | I |  |
0 |
1 |
0 |
0 |
| M2(15) | geen |  |
0 |
1 |
0 |
0 |
Boven: Tabel Modeltypen (blad 2)
Als een model M2 := (Ux, S, T) tot een modeltype behoort waar een 1 bij staat, is voor dat model de uitspraak "S = T" waar. Staat er een 0 bij het modeltype waartoe M2(i) behoort, dan is "S = T" onwaar.
DEFINITIE 21.16.: S ¹ T := S is ongelijk aan T := ¬(S = T).
¹ T volgt keurig uit die van S = T door toepassing van de logische semantiek van de waarheidsfunctie "¬": als S = T een 1 heeft, heeft S ¹ T een 0, als S = T een 0 heeft, heeft S ¹ T een 1.Toelichting: de waarheidskolom (5) van S
M.b.v. "
Æ" (definitie 21.10), "=" (definitie 21.15) en " ¹" (definitie 21.16) kun je prettig afkorten:| De Uitspraak | betekent hetzelfde als | maar ook hetzelfde als |
| er zijn I'tjes | $x(xÎS Ç T) | S Ç T ¹Æ |
| er zijn geen I'tjes | "x(x Ï SÇT) | SÇT =Æ |
| er zijn II'tjes | $x(xÎS \ T) | S \ T ¹ Æ |
| er zijn geen II'tjes | " x(x Ï S \ T) | S \ T =Æ |
| er zijn III'tjes | $x(xÎT \ S) | T \ S ¹Æ |
| er zijn geen III'tjes | " x(x Ï T \ S) | T \ S =Æ |
| er zijn IV'tjes | $x(xÎ |
|
| er zijn geen IV'tjes | v x(x Ï |
Tabel 21.5.
De formule |
Hetzelfde betekent als |
en ook als | en ook als |
$x(xÎS) |
¬"x(¬(xÎS)) |
{x |xÎS} ¹Æ | {x | ¬(xÎS)} ¹ Ux |
$x(¬(xÎS)) |
¬"x(xÎS) |
{x | ¬(xÎS)} ¹Æ | {x | xÎS} ¹ Ux |
¬$x(xÎS) |
"x(¬(xÎS)) |
{x | xÎS} =Æ | {x | ¬(xÎS)} = Ux |
¬$x(¬(xÎS)) |
"x(xÎS) |
{x | ¬(xÎS)} =Æ | {x | xÎS} = Ux |
Tabel 21.6.
Voor de volgende propositie is geen aparte definitie meer nodig:
21.2. S = ![]()
" x(xÎS«x Ï T). Er zijn geen I'tjes en geen IV'tjes (als bij M2(8)), want P«¬Q is volgens ' 8 zo te berekenen:Toelichting: S is het complement van T betekent (zie definitie 21.9.): S = Ux \ T (Ux zonder T). Een andere manier om hetzelfde te zeggen is:
| P | Q | ¬Q | P«¬Q | |
| I | 1 | 1 | 0 | 0 |
| II | 1 | 0 | 1 | 1 |
| III | 0 | 1 | 0 | 1 |
| IV | 0 | 0 | 1 | 0 |
Tabel 21.7.
I'tjes en IV'tjes ontbreken per definitie. Maar S =
16 is niet onwaar als ook II'tjes ontbreken zoals bij M2(3). Of III'tjes (M2(2)) of allebei (M2(0)). Bij de overige M2(i)'s staat in de waarheidskolom (6) van S =
een 0.
N.B. S = ![]() betekent dus iets anders dan S
betekent dus iets anders dan S
Ook geen nieuwe definitie is nodig voor:
21.3. Ux =
ÆToelichting: er zijn geen I'tjes, geen II'tjes, geen III'tjes en geen IV'tjes (zie definitie 21.1. en definitie 21.10.). Behalve M2(0) zijn alle modeltypen uitgesloten. Zie waarheidskolom (7) van tabel 21.3.
DEFINITIE 21.17.: S ![]() T := S en T overlappen
gedeeltelijk :=
T := S en T overlappen
gedeeltelijk :=
$x(xÎSÇT) & $x(xÎS \ T) & $x(xÎT \ S):=
Toelichting: hier zegt het definiëns letterlijk: er zijn I'tjes,
II'tjes en III'tjes, zoals bij M2 (11). Er wordt dus niet uitgesloten dat er
ook IV'tjes zijn zoals bij M2(15), maar ze mogen ontbreken. Alle andere M2(i)'s
krijgen een 0 in de waarheidskolom (8)van S ![]() T. S
T. S ![]() T
betekent hetzelfde als S
T
betekent hetzelfde als S
DEFINITIE 21.18.: S
ÊT := S omvat T := " x(xÎT®xÎS)' 8:Toelichting: Uit
| xÎS := P | xÎT := Q | Q®P | |
| I | 1 | 1 | 1 |
| II | 1 | 0 | 1 |
| III | 0 | 1 | 0 |
| IV | 0 | 0 | 1 |
Tabel 21.8.
" x(xÎT®xÎS) zegt dus: er zijn geen III'tjes. T \ S = i! Zoals in M2(12), maar ook in M2(i), i = 9, 7, 5, 4, 2, 1, 0. Daar komen dus enen te staan. In de overige modeltypen zitten modellen met III'tjes. Bij die modeltypen komt dus voor SÊT een 0 te staan. Zo krijgen we in tabel 21.2. waarheidskolom (9) van SÊT.
DEFINITIE 21.19.: SÉT := S omvat T echt := SÊT & S ¹ T
Toelichting: In tabel 21.2. is waarheidskolom (10) van SÉT is te berekenen uit (9) en (5) m.b.t. de logische semantiek van "&". Er blijven slechts 4 mogelijkheden over met een 1: M2(12), M2(9), waarin T =Æ, M2(5), en M2(2). Als S omvat T echt, dan moeten er x'en in Ux zitten: M2(0) krijgt ook een 0.
DEFINITIE 21.20.: SÍT := S is een deelverzameling van T := " x(xÎS®xÎT)
Toelichting uit par 8:
| xÎS := P | xÎT =: Q | P®Q | |
| I | 1 | 1 | 1 |
| II | 1 | 0 | 0 |
| III | 0 | 1 | 1 |
| IV | 0 | 0 | 1 |
Tabel 21.9.
" x(xÎS®xÎT) zegt dus: er zijn geen II'tjes, zoals in M2(i), i = 0, 1, 3, 4, 6, 7, 10 en 13. Op die rijen komt in waarheidskolom (11) van SÍT een 1. In de overige M2 (i) zitten modellen met II'tjes.
DEFINITIE 21.21.: S
ÌT := S is een echte deelverzameling van T := SÍT & S ¹ T.Toelichting: analoog aan definitie 21.19. Bedenk dit zelf. Zie waarheidskolom (12).
Tenslotte nog een propositie waarvoor we wél een woord, maar geen apart tekentje meer verzinnen:
21.4. S en T zijn disjunct := S
ÇT =ÆToelichting: Hier staat ronduit: er zijn geen I'tjes. Dat klopt voor M2(i), i = 0, 2, 3, 4, 8, 9, 10, 14. Bij de overige M2(i) moet dus een nul staan.
We hebben nu 10 waarheidskolomen ((4 t/m (13) van tabel 21.3.) uitgerekend op basis van
D 21.15. (S = T)
D 21.16. (S
¹ T)21.2. (S = ![]() )
)
21.3. (Ux =
Æ)D 21.17. (S ![]() T)
T)
D 21.18. (S
ÊT)D 21.19. (S
ÉT)D 21.20. (S
ÍT)D 21.21. (S
ÌT)21.4. (S
ÇT =Æ)De 16 modeltypen kunnen echter allemaal, onafhankelijk van elkaar, een 1 of
een 0 krijgen. Hoeveel waarheidskolommen zijn er dan in totaal?
216 = 65.536
Maar die andere 65.526 kun je nu zelf!
We hebben slechts voorbeelden behandeld van M2 := (Ux, S, T): dus er waren steeds maar twee verzamelingen voor Ux gedefinieerd.
Wat als het er drie zijn? Dus M3 := (Ux, S1, S2, S3)?
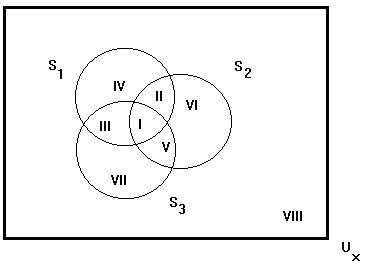
Dan zijn er modellen van een type dat I'tjes, II'tjes, ..., VIII'tjes heeft.
Hoeveel modeltypen zijn er dan?
28 = 256
Hoeveel waarheidskolommen zijn er dan?
2256
. 1, 157921 x 1077(Ik heb alleen de eerste 7 van 78 cijfers, dus het is een benadering). Maar er gebeurt nooit meer iets nieuws. Tenminste, ik geloof het niet!
Bij modellen Mm := (Ux, S1, S2, ..., Sm) zijn er
2m romeinse cijfertjes voor soorten dingen
![]() 24 modeltypen
24 modeltypen
![]() 25 waarheidskolommen.
25 waarheidskolommen.
Oefeningen
A) Reken de waarheidskolommen uit van de samengestelde proposities in het definiëns van definitie 21.6., definitie 21.7. en definitie 21.8. Vergelijk de gevallen waarin een nul in de waarheidskolom staat met de illustraties van deze definities. Je hebt het fout gedaan als er een 1 staat bij een niet gearceerd gedeelte, of een 0 bij een gearceerd gedeelte.
B) Werk bij definitie 21.2. t/m 21.21. de volgende procedure af:
1) Kijk of het een definite is van een woord of van een zin.
2) Als het een woord is: verzin er beelden van, dus maak voorstellingen die een voorbeeld zijn van het definiëndum. Zorg dat er tenminste één beeld bij is waarvan je gelooft dat het een object heeft (dat er een van bestaat), en dat er tenminste één beeld bij is waarvan je gelooft dat het niet bestaat, dat het dus geen object heeft.
Als het een zin is: vul dingen in voor de letters. Doe het tenminste één keer zo dat er een zin ontstaat waarvan je gelooft dat hij waar is. Doe het tenminste één keer zo dat er een zin ontstaat waarvan je gelooft dat hij onwaar is.
C) Doe hetzelfde voor (S = ![]() ) en (Ux =
) en (Ux =
ADVIES: Als je voor een voorbeeld een Ux
¹Æ moet kiezen, neem eerst een Ux = Â. Heb je een goed voorbeeld in Â, probeer dan iets niet-wiskundigs.D) Geef met behulp van de geleerde tekentjes een aanduiding van vak III op pagina 84.
Go to: Previous Section; Next Section