Bert hamminga Back to: Index: Teaching Docs: hamminga, B. (1997) Informatie, Waarheid en Werkelijkheid,inhoudsopgave; Go to: Previous Section; Next Section
Page title: 1. Wat een redeneervorm is; waar logica over gaat
De termen "logica", "formele logica", "symbolische logica" en "wiskundige logica" verwijzen alle naar de studie van redeneringen. De oude Grieken deden het al (o.a. Aristoteles, Euclides), en aan de middeleeuwse universiteiten werd deze traditie voortgezet.
De uitbreiding van de wiskundige kennis en methode, sinds de 17e eeuw (Descartes, Leibniz), gaf nieuwe impulsen aan het denken over wat een redenering is, en hoe een redenering moet verlopen. Bekende namen uit de periode sinds het eind van de vorig eeuw zijn Frege, Russel en G�del.
Eeuwenlang is de behandeling die Euclides (300 v. Chr., Egypte) aan de meetkunde gaf, het grote voorbeeld voor filosofen en wiskundigen geweest. Euclides leidde de stellingen (theorema's) van de meetkunde af uit axioma's (vooronderstellingen; postulaten).
In de tijd van Euclides waren al erg veel meetkundige stellingen bewezen, zoals de bekende stelling van Pythagoras (580 v. Chr. Griekenland). Maar het was een beetje een "rommeltje": ieder bewijs ging weer op een andere manier en wat een bewijs tot een echt bewijs maakte was niet echt precies afgesproken. Euclides liet zien dat de stellingen van de meetkunde allemaal op dezelfde manier bewezen konden worden, als je uitging van 10 axioma's of postulaten. Zo maakte hij van alle verschillende stukjes meetkunde van zijn tijd een geheel. Dat maakte grote indruk. Het blijft tot vandaag een van de belangrijkste prestaties van de logica.
In de tijd van Descartes (een Fransman uit de 17e eeuw, hij woonde het grootste deel van zijn actieve leven in Nederland) waren via de Arabieren de basisregels van de algebra met veel stellingen bekend geworden. Descartes bedacht onder andere hoe je een algebra�sche formule kunt maken die een geometrische figuur "beschrijft". Zo konden zelfs de Arabische algebra en de Antieke geometrie verenigd worden tot wat in de logica heet een consistent, deductief geheel. Geleidelijk werden meer stukken van het menselijk redeneren door logici met elkaar in verband gebracht. Nu zijn er zelfs logische modellen van het gewone redeneren van mensen met "niet", "en", "of", "als...dan.." en "alleen als...dan...". En ook aan het andere uiterste is al hard gewerkt: de logische structuur van de meest ingewikkelde wetenschappelijke theorie�n.
Hoe gaan logici te werk? Zij bestuderen redeneringen:

Het is de bedoeling dat een redenering een bewijs is van de stelling, uitgaande van de axioma's.
Logica bestudeert hoe zo'n redenering verloopt, niet alleen op het gebied van de meetkunde, maar ook op tal van andere gebieden, zoals het alledaagse redeneren in natuurlijke talen en redeneren in de rekenkunde en de wetenschap.
Omdat in eigenlijk alle vakken aan de universiteit erg veel wordt geredeneerd, en omdat daarbij zowel de gewone taal, als de meetkunde, als de rekenkunde wordt gebruikt, is het voor iedere student belangrijk om zich bewust te zijn van tenminste een aantal principes van de logica.
Maar over het nut van de geometrie staat in de Encyclopaedia Britannica de volgende anecdote over Euclides: Another anecdote relates that a student, probably in Alexandria, after learning the very first proposition in geometry, wanted to know what he would get by learning these things, whereupon Euclid called his slave and said, "Give him threepence since he must needs make gain by what he learns."
Laten we twee voorbeelden van redeneren bekijken, en ze gemakshalve toeschrijven aan twee economen, 1 en 2. Beiden vooronderstellen iets en komen dan, op grond van die vooronderstellingen, tot een conclusie.
De lonen stijgen (P)
Als de lonen stijgen (P), stijgen de prijzen (Q1)
Als de prijzen stijgen (Q1 ), daalt de afzet (R1)
Als de afzet daalt (R1 ), vallen er ontslagen (S1)
Dus: Er vallen ontslagen!
De lonen stijgen (P)
Als de lonen stijgen (P), stijgt de consumptie (Q2)
Als de consumptie stijgt (Q2), stijgt de afzet (R2)
Als de afzet stijgt (R2), komt er meer werk (S2)
Dus: Er komt meer werk!
Deze twee economen zijn het duidelijk met elkaar oneens, maar hun menigsverschil betreft bepaald niet de manier van redeneren. Die is precies gelijk. Laten we die redenering nu bekijken.
Gebruik makend van de letters, P, Q, R en S waarmee we de zinsdelen hebben aangeduid, en door een pijltje naar rechts te gebruiken als we "als ... dan ..." willen zeggen, komen we tot het volgende schema:
P
P � Q
Q � R vooronderstellingen
R � S
_____________
S conclusie
Waarom klopt deze redenering? Omdat er (herhaald) gebruik is gemaakt van een zgn. afleidingsregel waarvan de juistheid onmiddellijk duidelijk is:
uit "A" en "A � B" A A � B
volgt: "B" B
De streep "______" betekent: "ik pas nu de afleidingsregel toe". Het rechterschema is gewoon een afkorting van het linkerschema. Nu kan ik de redenering van de economen 1 en 2 zo weergeven.
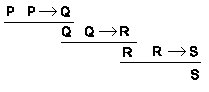
Deze afleidingsregel heet modus ponens en hij is drie keer gebruikt. Om van "P", "P �Q" naar "Q" te komen, om van "Q", "Q � R" naar "R" te komen en om van "R", "R �S" naar "S" te komen.Het antwoord op de vraag: "Waarom klopt deze redenering is dus: "omdat er op correcte wijze een afleidingsregel is toegepast die juist is".
Merk twee belangrijke zaken op.
1. Econoom 1 en econoom 2 kunnen heftig met elkaar debatteren over de werkgelegenheid, maar dat betreft dan niet hun redeneringen. Daarover zijn zij het volmaakt eens. Voor die redenering doet het er niet toe naar welke uitspraken de letters P, Q, R en S verwijzen. (R1 en R2 gaan allebei toevallig over afzet, maar Q1 gaat over prijzen en Q2 gaat over consumptie. Met "Q" bedoel ik dus eigenlijk niets m��r dan "de nazin van de tweede uitspraak van beide economen die tegelijk de voorzin van de derde uitspraak van beide economen is".) Het had net zo goed over tafelvoetbal kunnen gaat. Hun redenering klopt, en de reden daarvoor is NIET dat de vooronderstellingen waar zijn!
2. De redenering is correct, hij klopt, omdat het onmogelijk is dat de vooronderstellingen waar zijn en tegelijk de conclusie onwaar. Van een redenering die klopt kunnen de vooronderstellingen best onwaar zijn. De twee economen zullen de waarheid van elkaars vooronderstellingen betwisten. Ook kan er nog een derde langskomen die zegt dat de lonen dalen, dus dat de enige vooronderstellingen waarover de eerste twee het nog eens waren, niet waar is. Wat er ook waar of onwaar is in de vooronderstellingen, beide redeneringen blijven juist. Ter illustratie van een onjuiste redenering laten we de derde econoom eens een redeneerfout maken. Stel, hij beweert (we gebruiken "�" voor "niet").
Ik ben het eens met econoom 1 dat
als de lonen stijgen (P), dat dan de prijzen stijgen (Q1).
Maar de lonen stijgen niet (�P)
Dus: de prijzen stijgen niet (�Q1).
Ook econoom 3 past een afleidingsregel toe, maar die afleidingsregel is onjuist:
redenering econoom 3: toegepaste afleidingsregel :
![]()
De onjuistheid is snel in te zien: naast loonstijging zijn er talloze andere factoren die tot prijsstijging kunnen leiden, zoals slechte oogsten, een toename van de geldhoeveelheid die in omloop is, het opraken van bepaalde grondstoffen. Ook hier geldt weer: ik heb geen economie nodig om in te zien dat de redenering niet klopt. Een tegenvoorbeeld uit het tafelvoetbal is even overtuigend, als het er om gaat de onjuistheid van deze afleidingsregel te laten zien:
Wie bij het loslaten van de keepersstang de keeper scheef naast zijn doel zet (P), krijgt snel een goal tegen (Q)
Mijn keeper staat niet scheef naast zijn doel (�P)
Dus: Ik krijg niet snel een goal tegen (�Q)
Dit klopt niet, want als mijn tegenstander veel beter is zal het me niet veel helpen dat ik toevallig ��n ding goed doe: ik krijg toch snel een goal tegen. Zelfs al zou het waar blijken dat ik niet snel een goal tegen krijg, (en zelfs al zou het waar blijken dat de prijzen niet stijgen), dan nog zou deze redenering niet kloppen.
Om even een overzicht over de zaak te krijgen constateren we dat vooronderstellingen (dat zijn uitspraken) waar of onwaar kunnen zijn, dat een redenering (dat is dus niet een uitspraak) juist of onjuist kan zijn, en dat de conclusie waar of onwaar kan zijn. Dat is alle drie apart te controleren, zodat er in principe 8 gevallen moeten worden bekeken.
| Vooronderstellingen | Redenering | Conclusie |
| 1 Waar | Juist | Waar (kan voorkomen) |
| 2 Waar | Juist | Onwaar (KAN NIET VOORKOMEN) |
| 3 Waar | Onjuist | Waar (kan voorkomen) |
| 4 Waar | Onjuist | Onwaar (kan voorkomen) |
| 5 Onwaar | Juist | Waar (kan voorkomen) |
| 6 Onwaar | Juist | Onwaar (kan voorkomen) |
| 7 Onwaar | Onjuist | Waar (kan voorkomen) |
| 8 Onwaar | Onjuist | Onwaar (kan voorkomen) |
Tabel 1.1.
De kracht van een juiste redenering is dus niet dat hij altijd tot ware conclusies leidt (kijk maar naar geval 6).
De kracht voor een juiste redenering ligt ergens anders, nl. daarin dat hij nooit tot onware conclusies leidt als de vooronderstellingen waar zijn, dus daarin dat geval 2 nooit kan voorkomen.
Niemand hoeft zich te verbazen dat geval 2 nooit voorkomt. De logici zorgen ervoor dat afleidingsregels die ooit eens van een waar stel premissen tot een onware conclusie hebben geleid, onmiddellijk worden verwijderd. En in meer dan tweeduizend jaar logica is heel veel werk gedaan.
Voorbeelden: (als de x in de volgende voorbeelden het getal 3 is, dan weten we welke premissen en conclusies waar resp. onwaar zijn).
Geval 1: (x=3) (waar)
(x=3) � (x2=9) (waar)
______________________(klopt!)
(x2=9) (waar)
Geval 2: bestaat niet
Geval 3: (x=2) � (x2=4) (waar)
(x=2) (waar)
_________________(klopt niet!)
�(x2=4) (waar)
Geval 4: (x=-3) � (x2=9) (waar)
�(x=-3) (waar)
__________________(onjuist)
�(x2 =9) (onwaar)
Geval 5: (x=2) (onwaar)
(x=2) � (x2=9) (onwaar)
___________________(klopt!)
(x2=9) (waar)
Geval 6: (x=2) (onwaar)
(x=2) � (x2=8) (onwaar)
___________________(klopt!)
(x2=8) (onwaar)
Geval 7: (x2=9) � (x=4) (onwaar)
�(x2=9) (onwaar)
_____________________(onjuist)
�(x=4) (waar)
Geval 8: (x2=9) � (x=3) (onwaar: x=-3 kan ook)
�(x2 =9) (onwaar)
__________________(onjuist)
�(x=3) (onwaar)
Oefening
Verzin zelf enkele redeneringen waarin de enige juiste afleidingsregel die je nu kent, de modus ponens, wordt toegepast. Probeer voorbeelden te vinden van elk der 7 gevallen die kunnen voorkomen. Van welk geval is de redenering van econoom 1 een voorbeeld? En die van de economen 2 en 3?
Klik voor de antwoorden bij de oefeningen
Go to: Previous Section; Next Section