De indeling van alle volzinnen in vier soorten is een schone zaak, maar als er slechts propositielogisch ware, propositielogisch onware, niet-propositielogisch ware en niet-propositielogisch onware volzinnen zijn, waarom zouden wij dan ooit volzinnen uitspreken? Een pijnlijke vraag, te meer omdat we behoorlijk ver in de cursus zijn.

Als iedereen alles wist zou er nooit worden gesproken. Het uitspreken van een volzin is dus een teken dat er iets niet in orde is. Kennelijk is er iemand die iets niet weet, maar gelukkig is er iemand anders die het wel weet, en die spreekt dan een volzin uit, zodat alles toch nog goed komt. Als er ergens een informatiestroom loopt, dan is dat ter oplossing van een probleem. Je weet dus meteen dat er een probleem is, zoals je dat weet wanneer je koorts hebt. Informatie is als het ware de koorts van de kennisstructuur. Die is ziek, en door de informatie wordt hij weer beter. Als er met aan die structuur veel mankeert, barst het van de informatiestromen. En iedereen kent wel die kortstondige fantstische momenten dat alles in orde is. Dan hoeven we elkaar niets te vertellen. Informatie is dan niet nodig. Je zit bij elkaar en het is goed.

Als iemand niets weet, is voor hem dan alles denkbaar? Bepaald niet! Neem voor P de volzin: "Op 14 oktober 1806 legde Hegel in Jena de laatste hand aan "die Ph�nomenologie des Geistes"", en voor Q: "Op 14 oktober 1806 won Napoleon de slag bij Jena". Wat is er mogelijk voor wie hier niets over weet?

                    Tabel 12.1.

De serie van twee atomaire volzinnen (P, Q) kan tot waarheidsgroep I, II, III of IV behoren. Maar meer is niet mogelijk, want andere waarheidsgroepen kunnen niet bestaan omdat ze ondenkbaar zijn. Probeer anders maar eens!

DEFINITIE 12.1.: De verzameling van waarheidsgroepen waarvan het denkbaar is dat een serie atomaire volzinnen (P₁, P₂, ..., P_n) er toe behoort, zolang we niets weten over de waarheid van P₁, P₂, ..., P_n, noemen we de propositielogische ruimte van (P₁, P₂, ...P_n).

Toelichting: We hoeven het niet de "propositielogische ruimte van f (P₁, P₂, ... P_n)" te noemen, want deze ruimte hangt niet van f , de voegwijze, af.

Nu zeg ik: "P & �Q" (ik verklap nog niet of dit waar is).

                                                Tabel 12.2.

Jij weet nu: als P waar is en Q ook (de volzin f (P, Q): = P & �Q zit dus in waarheidsgroep I), dan heb ik gelogen, of ik heb me vergist. In ieder geval heb ik dan onwaarheid gesproken. Als f (P, Q) in groep III of IV zit heb ik ��k onwaarheid gesproken.

Mijn volzin geeft de informatie dat de serie van de twee volzinnen (P, Q) niet tot de waarheidsgroepen I, III of IV behoort. Het kan zijn dat de informatie niet klopt, maar ik geef die informatie.

Wat is de inhoud van een uitspraak? Wanneer heeft een uitspraak "veel inhoud" (m.a.w. wanneer is hij "sterk"?) Wanneer is een uitspraak "zwak", m.a.w. heeft hij "weinig inhoud"?

Laten wij eerst de meest zwakke soort uitspraak nemen. Een uitspraak die helemaal niets zegt. Een "lege" uitspraak:

P V �P

(P is nog steeds die volzin over Hegel) Waarom is deze uitspraak "zwak"? Waarom "zegt hij niets"? Waarom zou je hem "leeg" kunnen noemen? Waarom heeft hij, zoals we zullen gaan zeggen, geen "inhoud"? Omdat er geen enkel denkbaar geval is dat door P V �P wordt uitgesloten. P V �P heeft geen enkele nul in zijn waarheidskolom: Niet alleen P V �P, maar alle propositielogisch ware uitspraken zijn leeg. Ze hebben geen inhoud. Ze sluiten geen enkel denkbaar geval uit. Alle denkbare gevallen zijn mogelijk, want bij geen enkel denkbaar geval heeft een geldige formule een nul in zijn waarheidskolom. Juist daarom weten we zo zeker dat zo'n uitspraak waar is!

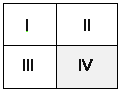
Maar om diezelfde reden leren we erg weinig van propositielogisch ware uitspraken: onze kennis over welke gevallen zich wel, en welke gevallen zich niet kunnen voordoen wordt er niet groter van. Laten we eens voorbeelden bekijken van formules die uit geen andere atomaire formules zijn samengesteld dan P en Q. Dan levert de waarheidstafel van P en Q ons krachtens definitie 12.1. een propositielogische ruimte, de verzameling van denkbare gevallen voor P en Q; de verzameling: {I, II, III, IV}. We kunnen die ruimte ook in een plaatje weergeven:

Een uitspraak als P V �P heeft in alle 4 gevallen een 1 in zijn waarheidskolom. Geen enkele mogelijkheid in de logische ruimte is dus uitgesloten als P V �P waar is. Hoe anders is dat met P V Q (het gaat nog steeds over Hegel en Napeleon)? Weliswaar zijn geval I, II en III mogelijk, en weten we op basis van P V Q niet welk van deze drie gevallen zich voordoet, maar ��n geval kan zich, als P V Q waar is, niet voordoen: IV.

P V Q heeft dus inhoud. En die inhoud bestaat uit geval IV:

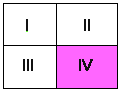
Slordig gezegd bestaat de inhoud van een uitspraak uit: wat volgens die uitspraak onmogelijk waar kan zijn. Als zoiets toch waar is, hebben we verkeerde informatie gekregen. P V �P gaf ons geen gelegenheid te kiezen uit I, II, III en IV. P V Q geeft ons geen gelegenheid te kiezen uit I, II en III. Het witte gebied in het plaatje van de logische ruimte is dus juist niet de inhoud. Wat wit is, is nog mogelijk. Wat grijs is, is uitgesloten.

Nu nemen we P & Q

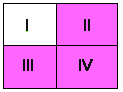
Nu zijn op ��n na alle gevallen uitgesloten. All��n I is nog mogelijk. We noemen P & Q sterker dan P V Q omdat P & Q twee extra gevallen uitsluit: II en III. We noemen P V Q zwakker dan P & Q. We zullen gaan zeggen dat de inhoud van P & Q de inhoud van P V Q omvat. Je kunt een uitspraak z� sterk maken dat je "te ver doorschiet", zoals bij P & �P. Dit is het plaatje van P & �P:

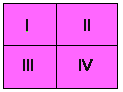
Nu zijn alle denkbare gevallen uitgesloten. (In de formule P & �P komt Q niet eens voor! Een voorbeeld met P �n Q die hetzelfde volledige grijze plaatje heeft, is: (P V Q) & �(P V Q.)) Je leert dus kennelijk het meest van de "��n na sterkste uitspraak". Want de allersterkste uitspraken zijn de inconsistente uitspraken, en daarvan weten we van te voren dat ze in alle gevallen onwaar zijn, dus heeft het geen zin meer om je af te vragen hoe de wereld er uit zou zien als hij waar was. Dat is ondenkbaar.

DEFINITIE 12.2. De "inhoud I(B) van een formule B = f (P₁, P₂, .., P_n) is de verzameling van die waarheidsgroepen van (P₁, P₂, .., P_n), waarvoor de waarheidskolom van f (P₁, P₂, .., P_n) een nul heeft.

We hebben dus gezien dat

Als het belangrijk is, spreken we verschillende woorden af voor formules (bijvoorbeeld: "geldig") en hun volzinnen ("propositielogisch waar"). Maar hier maakt het niets uit, dus, we zeggen gewoon

DEFINITIE 12.3. Volzin A noemen we sterker (zwakker) dan volzin B als formule A sterker (zwakker) is dan formule B.

(Je moet er niet van schrikken dat er nu eens over bijvoorbeeld "formule A = P V �P", en dan weer over "volzin A = P V �P" wordt gesproken. Het is net als in de wiskunde, daar spreken ze ook over de functie x² + 1 en het getal x² + 1: "Voor alle getallen x is het getal x² + 1 positief" en: "De functie x² + 1 is definiet positief").

Laten we eens een beetje wijsgerig doen: als je volstrekte zekerheid wilt, zijn propositielogisch ware uitspraken het meest begeerlijk. Maar die geven ons geen enkele informatie. Als we informatie willen, zijn sterke uitspraken het meest begeerlijk. Maar die kunnen onwaar zijn. Zo is het leven.

Denk daarbij eens aan het volgende: een adviseur zal tegen zijn klant niet louter propopitielogisch ware uitspraken kunnen doen. Dan loopt de klant weg. Zijn uitspraken moeten dus enige informatie bevatten. Een klant wil zoveel mogelijk informatie. De adviseur echter wil zo weinig mogelijk risico lopen iets te zeggen dat verkeerd uitpakt. Dat is niet goed voor zijn zaak. Dus de adviseur geeft een hoeveelheid informatie die juist genoeg is om de klant zijn portemonnee te laten trekken. Bij elke klant zal dat opnieuw wikken en wegen zijn.

Er zijn heel veel uitspraken waarvan de inhoud niet vergeleken kan worden. Bijvoorbeeld P V �Q en �P V Q:

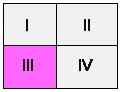
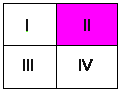
Maar ook P & �Q en �P & Q

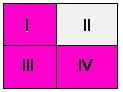
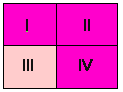
P V �Q en �P V Q zijn onvergelijkbaar in sterkte

P & �Q en �P & Q zijn onvergelijkbaar in sterkte

P V �Q en �P & Q zijn onvergelijkbaar in sterkte, hoewel P V �Q slechts ��n 0 heeft en �P & Q drie nullen heeft. "M��r nullen" betekent dus niet altijd: sterker. Maar een formule met meer nullen kan nooit zwakker zijn. "Onvergelijkbaar in sterkte" betekent dat je niet kunt bepalen welke de sterkste is.

Dat is dus iets anders dan even sterk: P & Q en ��P & ��Q zijn bijvoorbeeld even sterk:

We maken de volgende afspraken.

We illustreren de begrippen nog even met een schema:

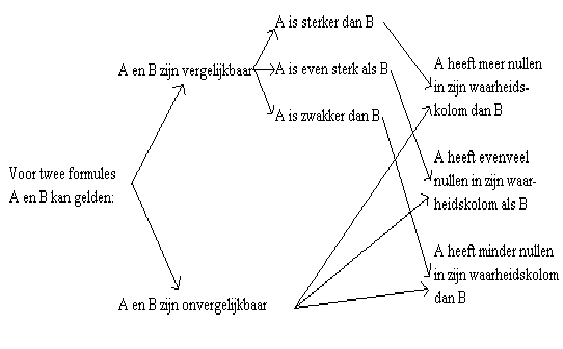
Oefening

Veel van de in deze paragraaf gebruikte voorbeelden van formules met all��n P en Q zijn nog niet onderling vergeleken.Doe dit.

Klik voor de antwoorden bij de oefeningen

Go to: Previous Section; Next Section